说明
快速排序(QuickSort),又称分区交换排序(partition-exchange sort),简称快排。快排是一种通过基准划分区块,再不断交换左右项的排序方式,其采用了分治法,减少了交换的次数。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归或迭代进行,以此让整个数列变成有序序列。
实现过程
- 在待排序区间找到一个基准点(pivot),便于理解一般是位于数组中间的那一项。
- 逐个循环数组将小于基准的项放左侧,将大于基准的项放在右侧。一般通过交换的方式来实现。
- 将基准点左侧全部项和基点右侧全部项分别通过递归(或迭代)方式重复第1项,直到所有数组都交换完成。
示意图
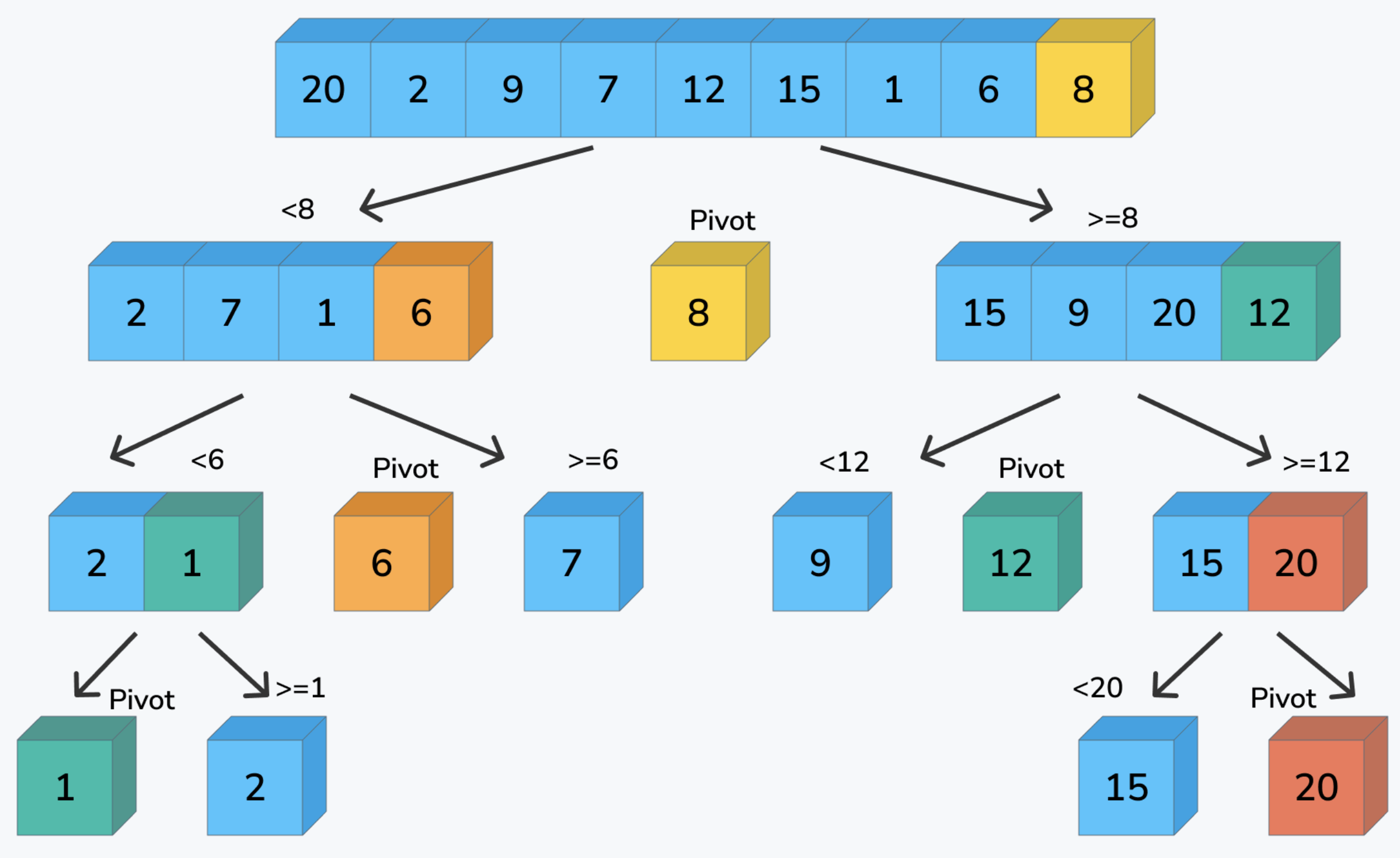
解释:以某个数字为基点,这里取最右侧的数字8,以基点划分为两个区间,将小于8的数字放在左侧区间,将大于8的数字放在右侧区间。再将左侧区间和右侧区间分别放到递归,按照最右侧为基点,继续分解。直到分解完毕,排序完成。这是其中一种常见的分区递归法,除了这种方式外,还有其他实现方式。
性能分析
平均时间复杂度:O(NlogN)
最佳时间复杂度:O(NlogN)
最差时间复杂度:O(N^2)
空间复杂度:根据实现方式的不同而不同,可以查看不同版本的源码
代码快排方式1, 新建数组递归版本。无需交换,每个分区都是新数组,数量庞大。
这个版本利用了JS数组可变且随意拼接的特性,让每个分区都是一个新数组,从而无需交换数组项。
这个方式非常简单易懂,但理论上来讲不是完全意义上的快排,效率较差。
function quickSort1(arr) { // 数组长度为1就不再分解 console.log('origin array:', arr) if (arr.length <= 1) { return arr } var pivot const left = [] const right = [] // 设置中间数,取最中间的项 var midIndex = Math.floor(arr.length / 2) pivot = arr[midIndex] for (var i = 0, l = arr.length; i < l; i++) { console.log('i=' + i + ' midIndex=' + midIndex + ' pivot=' + pivot + ' arr[]=' + arr) // 当中间基数等于i时跳过。基数数待递归完成时合并到到新数组。 if (midIndex === i) { continue } // 当前数组里面的项小于基数则添加到左侧 if (arr[i] < pivot) { left.push(arr[i]) // 大于等于则添加到右侧 } else { right.push(arr[i]) } } arr = quickSort1(left).concat(pivot, quickSort1(right)) console.log('sorted array:', arr) // 递归调用遍历左侧和右侧,再将中间值连接起来 return arr}
递归的过程
// 基于中间位置进行递归分解: f([7, 11, 9, 10, 12, 13, 8]) / 10 \ f([7, 9, 8]) f([11, 12, 13]) / 9 \ / 12 \ f([7, 8]) f([]) f([11]) f[13] / 8 \f([7]) f([]) [7]// 将递归后的最小单元和基数连接起来// 得到:[7, 8, 9, 10, 11, 12, 13]
快排方式2, 标准分区递归版本。左右分区递归交换排序,无需新建数组。
这个版本是最常见的标准分区版本,简单好懂。先写一个分区函数,依据基准值把成员项分为左右两部分。基准值可以是数列中的任意一项,为了交换方便,基准值一般最左或最右侧项。把小于基准值的放在左侧,大于基准值的放在右侧,最后返回分区索引。这样就得到一个基于基准值的左右两个部分。再将左右两个部分,分别进行分区逻辑的递归调用,当左右值相等,也就是最小分区只有1项时终止。
// 分区函数,负责把数组分按照基准值分为左右两部分// 小于基准的在左侧,大于基准的在右侧最后返回基准值的新下标function partition(arr, left, right) { // 基准值可以是left与right之间的任意值,再将基准值移动至最左或最右即可。 // 直接基于中间位置排序,则需要基于中间位置左右交换,参加基于中间位置交换的版本。 // var tmpIndex = Math.floor((right - left) / 2) // ;[arr[left + tmpIndex], arr[right]] = [arr[right], arr[left + tmpIndex]] var pivotIndex = right var pivot = arr[pivotIndex] var partitionIndex = left - 1 for (var i = left; i < right; i++) { // 如果比较项小于基准值则进行交换,并且分区索引增加1位 // 也就是将大于基准值的全部往右侧放,以分区索引为分割线 if (arr[i] < pivot) { partitionIndex++ if (partitionIndex !== i) { [arr[partitionIndex], arr[i]] = [arr[i], arr[partitionIndex]] } } } partitionIndex++; [arr[partitionIndex], arr[pivotIndex]] = [arr[pivotIndex], arr[partitionIndex]] return partitionIndex}// 分区递归版本,分区递归调用。function quickSort2(arr, left, right) { left = left !== undefined ? left : 0 right = right !== undefined ? right : arr.length - 1 if (left < right) { var pivot = partition(arr, left, right) quickSort2(arr, left, pivot - 1) quickSort2(arr, pivot + 1, right) } return arr}
快排方式3, 标准左右交换递归版本。基于中间位置不断左右交换,无需新建数组。
此版本基于中间位置,建立双指针,同时从前往后和从后往前遍历,从左侧找到大于基准值的项,从右侧找到小于基准值的项。
再将大于基准值的挪到右侧,将小于基准值的项挪到左侧,直到左侧位置大于右侧时终止。左侧位置小于基准位置则递归调用左侧区间,右侧大于基准位置则递归调用右侧区间,直到所有项排列完成。
function quickSort3(arr, left, right) { var i = left = left !== undefined ? left : 0 var j = right = right !== undefined ? right : arr.length - 1 // 确定中间位置,基于中间位置不停左右交换 var midIndex = Math.floor((i + j) / 2) var pivot = arr[midIndex] // 当左侧小于等于右侧则表示还有项没有对比,需要继续 while (i <= j) { // 当左侧小于基准时查找位置右移,直到找出比基准值大的位置来 while (arr[i] < pivot) { console.log('arr[i] < pivot:', ' i=' + i + ' j=' + j + ' pivot=' + pivot) i++ } // 当前右侧大于基准时左移,直到找出比基准值小的位置来 while (arr[j] > pivot) { console.log('arr[j] > pivot:', ' i=' + i + ' j=' + j + ' pivot=' + pivot) j-- } console.log(' left=' + left + ' right=' + right + ' i=' + i + ' j=' + j + ' midIndex=' + midIndex + ' pivot=' + pivot + ' arr[]=' + arr) // 当左侧位置小于等于右侧时,将数据交换,小的交换到基准左侧,大的交换到右侧 if (i <= j) { [arr[i], arr[j]] = [arr[j], arr[i]] // 缩小搜查范围,直到左侧都小于基数,右侧都大于基数 i++ j-- } } // 左侧小于基数位置,不断递归左边部分 if (left < j) { console.log('left < j:recursion: left=' + left + ' right=' + right + ' i=' + i + ' j=' + j + 'arr[]' + arr) quickSort3(arr, left, j) } // 基数位置小于右侧,不断递归右侧部分 if (i < right) { console.log('i < right:recursion: left=' + left + ' right=' + right + ' i=' + i + ' j=' + j + 'arr[]' + arr) quickSort3(arr, i, right) } return arr}
快排方式4, 非递归左右交换版本。基于中间位置不断左右交换,利用stack或queue遍历。
这种方式标准左右交换递归版本的非递归版本,其原理一样,只是不再递归调用,而是通过stack来模拟递归效果。这种方式性能最好。
function quickSort4(arr, left, right) { left = left !== undefined ? left : 0 right = right !== undefined ? right : arr.length - 1 var stack = [] var i, j, midIndex, pivot, tmp // 与标准递归版相同,只是将递归改为遍历栈的方式 // 先将左右各取一个入栈 stack.push(left) stack.push(right) while (stack.length) { // 如果栈内还有数据,则一并马上取出,其他逻辑与标准递归版同 j = right = stack.pop() i = left = stack.pop() midIndex = Math.floor((i + j) / 2) pivot = arr[midIndex] while (i <= j) { while (arr[i] < pivot) { console.log('arr[i] < pivot:', ' i=' + i + ' j=' + j + ' pivot=' + pivot + 'arr[]=' + arr) i++ } while (arr[j] > pivot) { console.log('arr[j] > pivot:', ' i=' + i + ' j=' + j + ' pivot=' + pivot + 'arr[]=' + arr) j-- } if (i <= j) { tmp = arr[j] arr[j] = arr[i] arr[i] = tmp i++ j-- } } if (left < j) { // 与递归版不同,这里当左侧小于基数位置时添加到栈中,以便继续循环 console.log('left < j:recursion: left=' + left + ' right=' + right + ' i=' + i + ' j=' + j + 'arr[]=' + arr) stack.push(left) stack.push(j) } if (i < right) { // 当右侧大于等于基数位置时添加到栈中,以便继续循环 console.log('i < right:recursion: left=' + left + ' right=' + right + ' i=' + i + ' j=' + j + 'arr[]=' + arr) stack.push(i) stack.push(right) } } return arr}
测试
(function () { const arr = [7, 11, 9, 10, 12, 13, 8] // 构建数列,可以任意构建,支持负数,也不限浮点 // const arr = [17, 31, 12334, 9.545, -10, -12, 1113, 38] console.time('sort1') const arr1 = arr.slice(0) console.log('sort1 origin:', arr1) console.log('\r\nquickSort1 sorted:', quickSort1(arr1)) console.timeEnd('sort1') console.time('sort2') const arr2 = arr.slice(0) console.log('sort2 origin:', arr2) console.log('\r\nquickSort2 sorted:', quickSort2(arr2)) console.timeEnd('sort2') console.time('sort3') const arr3 = arr.slice(0) console.log('sort3 origin:', arr3) console.log('\r\nquickSort3 sorted:', quickSort3(arr3)) console.timeEnd('sort3') console.time('sort4') const arr4 = arr.slice(0) console.log('sort4 origin:', arr4) console.log('\r\nquickSort4 sorted:', quickSort4(arr4)) console.timeEnd('sort4')})()/**// 测试结果jarry@jarrys-MacBook-Pro quicksort % node quick_sort.jssort1 origin: [ 7, 11, 9, 10, 12, 13, 8]origin array: [ 7, 11, 9, 10, 12, 13, 8]i=0 midIndex=3 pivot=10 arr[]=7,11,9,10,12,13,8i=1 midIndex=3 pivot=10 arr[]=7,11,9,10,12,13,8i=2 midIndex=3 pivot=10 arr[]=7,11,9,10,12,13,8i=3 midIndex=3 pivot=10 arr[]=7,11,9,10,12,13,8i=4 midIndex=3 pivot=10 arr[]=7,11,9,10,12,13,8i=5 midIndex=3 pivot=10 arr[]=7,11,9,10,12,13,8i=6 midIndex=3 pivot=10 arr[]=7,11,9,10,12,13,8origin array: [ 7, 9, 8 ]i=0 midIndex=1 pivot=9 arr[]=7,9,8i=1 midIndex=1 pivot=9 arr[]=7,9,8i=2 midIndex=1 pivot=9 arr[]=7,9,8origin array: [ 7, 8 ]i=0 midIndex=1 pivot=8 arr[]=7,8i=1 midIndex=1 pivot=8 arr[]=7,8origin array: [ 7 ]origin array: []sorted array: [ 7, 8 ]origin array: []sorted array: [ 7, 8, 9 ]origin array: [ 11, 12, 13 ]i=0 midIndex=1 pivot=12 arr[]=11,12,13i=1 midIndex=1 pivot=12 arr[]=11,12,13i=2 midIndex=1 pivot=12 arr[]=11,12,13origin array: [ 11 ]origin array: [ 13 ]sorted array: [ 11, 12, 13 ]sorted array: [ 7, 8, 9, 10, 11, 12, 13]quickSort1 sorted: [ 7, 8, 9, 10, 11, 12, 13]sort1: 9.824mssort2 origin: [ 7, 11, 9, 10, 12, 13, 8]partitioned arr= [ 7, 8, 9, 10, 12, 13, 11] partitionIndex: 1 left= [ 7 ] arr[partitionIndex]= 8 right= [ 8, 9, 10, 12, 13, 11 ] [ 7, 8, 9, 10, 12, 13, 11]partitioned arr= [ 7, 8, 9, 10, 11, 13, 12] partitionIndex: 4 left= [ 9, 10 ] arr[partitionIndex]= 11 right= [ 11, 13, 12 ] [ 7, 8, 9, 10, 11, 13, 12]partitioned arr= [ 7, 8, 9, 10, 11, 13, 12] partitionIndex: 3 left= [ 9 ] arr[partitionIndex]= 10 right= [ 10 ] [ 7, 8, 9, 10, 11, 13, 12]partitioned arr= [ 7, 8, 9, 10, 11, 12, 13] partitionIndex: 5 left= [] arr[partitionIndex]= 12 right= [ 12, 13 ] [ 7, 8, 9, 10, 11, 12, 13]quickSort2 sorted: [ 7, 8, 9, 10, 11, 12, 13]sort2: 1.15mssort3 origin: [ 7, 11, 9, 10, 12, 13, 8]arr[i] < pivot: i=0 j=6 pivot=10 left=0 right=6 i=1 j=6 midIndex=3 pivot=10 arr[]=7,11,9,10,12,13,8arr[i] pivot: i=3 j=5 pivot=10arr[j] > pivot: i=3 j=4 pivot=10 left=0 right=6 i=3 j=3 midIndex=3 pivot=10 arr[]=7,8,9,10,12,13,11left < j:recursion: left=0 right=6 i=4 j=2arr[]7,8,9,10,12,13,11arr[i] pivot: i=1 j=2 pivot=8 left=0 right=2 i=1 j=1 midIndex=1 pivot=8 arr[]=7,8,9,10,12,13,11i < right:recursion: left=0 right=6 i=4 j=2arr[]7,8,9,10,12,13,11arr[i] < pivot: i=4 j=6 pivot=13 left=4 right=6 i=5 j=6 midIndex=5 pivot=13 arr[]=7,8,9,10,12,13,11left < j:recursion: left=4 right=6 i=6 j=5arr[]7,8,9,10,12,11,13 left=4 right=5 i=4 j=5 midIndex=4 pivot=12 arr[]=7,8,9,10,12,11,13quickSort3 sorted: [ 7, 8, 9, 10, 11, 12, 13]sort3: 0.595mssort4 origin: [ 7, 11, 9, 10, 12, 13, 8]arr[i] < pivot: i=0 j=6 pivot=10arr[]=7,11,9,10,12,13,8arr[i] pivot: i=3 j=5 pivot=10arr[]=7,8,9,10,12,13,11arr[j] > pivot: i=3 j=4 pivot=10arr[]=7,8,9,10,12,13,11left < j:recursion: left=0 right=6 i=4 j=2arr[]=7,8,9,10,12,13,11i < right:recursion: left=0 right=6 i=4 j=2arr[]=7,8,9,10,12,13,11arr[i] < pivot: i=4 j=6 pivot=13arr[]=7,8,9,10,12,13,11left < j:recursion: left=4 right=6 i=6 j=5arr[]=7,8,9,10,12,11,13arr[i] pivot: i=1 j=2 pivot=8arr[]=7,8,9,10,11,12,13quickSort4 sorted: [ 7, 8, 9, 10, 11, 12, 13]sort4: 0.377ms */
链接
多种语言实现快速排序算法源码:https://github.com/microwind/algorithms/tree/master/sorts/quicksort
其他排序算法源码:https://github.com/microwind/algorithms