「学习笔记」平衡树基础:Splay 和 Treap
点击查看目录
目录
- 「学习笔记」平衡树基础:Splay 和 Treap
- 知识点
- 平衡树概述
- Splay
- 旋转操作
- Splay 操作
- 插入 \(x\)
- 查询排名为 \(k\) 的数
- 查询 \(x\) 的排名
- 查询 \(x\) 的前驱
- 查询 \(x\) 的后继
- 删除 \(x\)
- 代码
- 替罪羊树
- Treap
- FHQ_Treap
- 树套树
- 平衡树的区间操作
- 例题
- P3391 文艺平衡树
- 思路
- P4036 [JSOI2008]火星人
- 思路
- P4309 [TJOI2013]最长上升子序列
- 思路
- 星系探索
- 思路
- 代码
知识点平衡树概述
二叉搜索树(BST)的简单定义:
- 根节点的左子树权值 \(<\) 根节点权值 \(<\) 根节点的右子树权值;
- 左子树和右子树均为二叉搜索树。
这样的数据结构可以维护一个集合的以下操作:
- 查找最小/最大值;
- 插入一个元素;
- 删除一个元素;
- 求元素的排名;
- 查找排名为 \(k\) 的元素。
该数据结构最优情况下单次查询仅需 \(\Theta(\log_2{n})\) 的时间复杂度,但通过构造输入可以使二叉搜索树退化为链,达到 \(\Theta(n)\) 的时间复杂度。
所以我们要让这棵二叉搜索树尽量平衡(深度接近 \(\log_2{n}\))。
于是就诞生了平衡树。
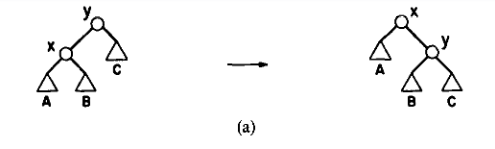
Splay旋转操作

可以发现左旋/右旋后树的形态发生变化,但仍然满足二叉搜索树的性质。
Splay 操作
Splay 的核心操作,即把一个点提到根。
分三种情况:
- 爹就是根:直接转(\(\text{zig}\))

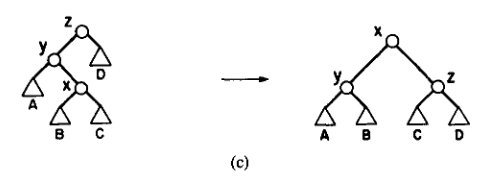
- 三点共线:先转爹,再转自己(\(\text{zig-zig}\))

- 三点不共线:直接转两下自己(\(\text{zig-zag}\)):

为什么要这么转呢?因为直接单旋上去无法保证复杂度,随随便便就能卡掉,而双旋的时间复杂度可以用势能分析法进行分析。
插入 \(x\)
根据 BST 的性质找到一个地方插入新点,然后把它旋上去。
查询排名为 \(k\) 的数
假设当前到了点 \(p\):
- \(k\) 小于 \(p\) 的左子树大小时往左走
- 否则令 \(k\) 减去 \(p\) 的左子树大小,然后:
- 如果当前节点副本数大于等于 \(k\),则当前节点的权值就是答案,然后把这个点旋上去。
- 否则令 \(k\) 减去 \(p\) 的副本数。
查询 \(x\) 的排名
找到 \(x\) 提到根,左子树的大小加 \(1\) 就是答案。
查询 \(x\) 的前驱
把 \(x\) 提到根后,在左子树里一路往右走。
查询 \(x\) 的后继
把 \(x\) 提到根后,在右子树里一路往左走。
删除 \(x\)
最麻烦的一个。
首先我们把 \(x\) 提到根
- 此时如果 \(x\) 副本数大于 \(1\) 则直接让副本数减一。
- 否则看儿子数量:
- 没儿子了:直接删。
- 一个儿子:让儿子当根。
- 两个儿子:首先把 \(x\) 的前驱提上来,因为刚才 \(x\) 是根并且最后一次旋转的时候不可能三点共线(不然就不是左子树的最大值了),所以此时根的右儿子是 \(x\),且此时 \(x\) 无左儿子,所以直接把 \(x\) 的右儿子接到根的右儿子上就可以了。
代码
点击查看代码
const ll N = 2e5 + 10, INF = 1ll << 40;namespace Splay {class TreePoint {public:ll val, cnt, sz;ll fa, son[2];inline void New (ll num) { val = num, cnt = sz = 1, fa = son[0] = son[1] = 0; return; }inline void Clear () { val = cnt = sz = fa = son[0] = son[1] = 0; return; }};class splay {public:TreePoint tr[N];ll tot = 0, rt = 0;#define va(p) tr[p].val#define cn(p) tr[p].cnt#define sz(p) tr[p].sz#define fa(p) tr[p].fa#define so(p, lr) tr[p].son[lr]inline void PushUp (ll p) { sz (p) = sz (so (p, 0)) + sz (so (p, 1)) + cn (p); return; } // Update the size.inline bool Get (ll p) { return p == so (fa (p), 1); } // Left son(0) or right son(1)?inline ll NewPoint (ll num) { tr[++tot].New (num); return tot; } // Build a new Point.inline void Rotate (ll p) {ll q = fa (p), r = fa (q), sd = Get (p);so (q, sd) = so (p, sd ^ 1);if (so (p, sd ^ 1)) fa (so (p, sd ^ 1)) = q;so (p, sd ^ 1) = q, fa (q) = p, fa (p) = r;if (r) so (r, q == so (r, 1)) = p;PushUp (q), PushUp (p);return;} // Zig or zag.inline void Splay (ll p) {for (ll q = fa (p); q = fa (p), q; Rotate (p))if (fa (q)) Rotate (Get (p) == Get (q) ? q : p);rt = p;return;} // Splay's core operations!inline void Out () {_for (i, 1, tot) {printf ("%lld : val=%lld cnt=%lld sz=%lld fa=%lld %lld %lld\n", i, va (i), cn (i), sz (i), fa (i), so (i, 0), so (i, 1));}puts ("");return;} // For debug.inline void Insert (ll x) {if (!rt) rt = NewPoint (x), PushUp (rt);else {ll p = rt;while (1) {ll sd = (bool)(va (p) < x);if (va (p) == x) {++cn (p);PushUp (p), PushUp (fa (p));break;}else if (so (p, sd)) p = so (p, sd);else {so (p, sd) = NewPoint (x);fa (so (p, sd)) = p, p = so (p, sd);PushUp (p), PushUp (fa (p));break;}}Splay (p);}return;} // Insert a number x.inline ll GetRank (ll x) {ll p = rt, cnt = 1;while (p) {if (va (p) <= x) {cnt += sz (so (p, 0));if (va (p) == x) break;cnt += cn (p);p = so (p, 1);}else p = so (p, 0);}Splay (p);return cnt;} // Get x's rank.inline ll GetKth (ll x) {ll p = rt;while (p) {if (sz (so (p, 0)) = x) break;x -= cn (p);p = so (p, 1);}else p = so (p, 0);}Splay (p);return va (p);} // Get k-th number.inline ll RealPre () {ll p = so (rt, 0);if (p) {while (so (p, 1)) p = so (p, 1);Splay (p);}return p;}inline void Delete (ll x) {GetRank (x);ll sd = (bool)(so (rt, 1));if (cn (rt) > 1) --cn (rt), PushUp (rt);else if (!so (rt, 0) && !so (rt, 1)) tr[rt].Clear (), rt = 0;else if (so (rt, 0) && so (rt, 1)) {ll p = rt, q = RealPre ();fa (so (p, 1)) = q;so (q, 1) = so (p, 1);tr[p].Clear ();PushUp (rt);}else {ll q = so (rt, sd);tr[rt].Clear ();fa (rt = q) = 0;}return;} // Delete a number x.inline ll Pre (ll x) {Insert (x);ll ans = va (RealPre ());Delete (x);return ans;} // Get x's pre.inline ll Next (ll x) {Insert (x);ll p = so (rt, 1), ans = 0;if (p) {while (so (p, 0)) p = so (p, 0);Splay (p);}ans = va (rt);Delete (x);return ans;} // Get x's next.#undef va#undef cn#undef sz#undef fa#undef so};}替罪羊树
很暴力的一个东西。
定义一个平衡因子 \(\alpha\)(最好选 \(0.7\sim0.8\)),插入/删除一个节点的时候检查是否存在一个节点的子树的大小乘上 \(\alpha\) 小于左/右儿子树的大小,如果有则把这棵子树直接拍平重构。
其他操作和普通 BST 一样。
点击查看代码
namespace ScapeGoatTree {const ldb alpha = 0.75;const ll N = 1e5 + 10;class TreePoint {public:ll val, cnt, sz, cp, del;ll fa, son[2];};class SGT {private:ll tot = 0, rt = 0, dp[N], cd = 0;TreePoint tr[N];vec tmp, c;#define va(p) tr[p].val#define cn(p) tr[p].cnt#define sz(p) tr[p].sz#define de(p) tr[p].del#define cp(p) tr[p].cp#define fa(p) tr[p].fa#define so(p, lr) tr[p].son[lr]inline ll NewP (ll num) {ll p = cd ? dp[cd--] : ++tot;va (p) = num;cn (p) = sz (p) = 1;cp (p) = fa (p) = so (p, 0) = so (p, 1) = de (p) = 0;return p;}inline void DelP (ll p) {va (p) = cn (p) = sz (p) = cp (p) = fa (p) = so (p, 0) = so (p, 1) = de (p) = 0;dp[++cd] = p;return;}inline void PushUp (ll p) {sz (p) = (de (p) ? 0 : cn (p)) + sz (so (p, 0)) + sz (so (p, 1));cp (p) = 1 + cp (so (p, 0)) + cp (so (p, 1));return;}public:inline void Clap (ll p) {if (so (p, 0)) Clap (so (p, 0));if (!de (p)) tmp.push_back (va (p)), c.push_back (cn (p));if (so (p, 1)) Clap (so (p, 1));DelP (p);return;}inline ll PullUp (ll l, ll r, ll fat) {if (l > r) return 0;bdmd;ll p = NewP (tmp[mid]);cn (p) = c[mid], fa (p) = fat;if (l < mid) so (p, 0) = PullUp (l, mid - 1, p);if (mid cp (p) * alpha || cp (so (p, 1)) > cp (p) * alpha;}inline void Check (ll p) {ll q = 0;while (p) {if (Bad (p)) q = p;rt = p;PushUp (p);p = fa (p);}if (q) ReBuild (q);return;}inline void Insert (ll num) {ll p = rt;if (!rt) {rt = NewP (num);return;}while (1) {if (va (p) == num) {++cn (p);if (de (p)) de (p) = 0;Check (p);return;}ll sd = num > va (p);if (so (p, sd)) p = so (p, sd);else {so (p, sd) = NewP (num);fa (so (p, sd)) = p;Check (p);return;}}return;}inline void Delete (ll num) {ll p = rt;while (p) {if (va (p) == num) {--cn (p);if (cn (p) va (p);p = so (p, sd);}return;}inline ll GetRank (ll num) {ll p = rt, rk = 1;while (p) {if (va (p) > num) {p = so (p, 0);continue;}rk += sz (so (p, 0));if (num == va (p)) break;rk += cn (p);p = so (p, 1);}return rk;}inline ll GetKth (ll k) {ll p = rt;while (p) {if (sz (so (p, 0)) >= k) {p = so (p, 0);continue;}k -= sz (so (p, 0));if (k <= cn (p)) break;k -= cn (p);p = so (p, 1);}return va (p);}inline ll Pre (ll num) { return GetKth (GetRank (num) - 1); }inline ll Nxt (ll num) { return GetKth (GetRank (num + 1)); }#undef va#undef cn#undef sz#undef de#undef cp#undef fa#undef so};}Treap
每个节点还要存一个随机权值,使得整棵树不仅对于原权值来说是一棵 BST,对于随机权值来说还是一个堆,在随机状态下一棵 Treap 是比较 \(\log_2n\) 层的。当然不排除你脸太黑导致 Treap 退化成链的极小可能。
那么插入的时候,如果新节点不满足堆的性质了,需要往上旋转。删除的时候直接旋到叶子结点删掉,或者只剩一个儿子的时候直接让儿子代替自己。
其他操作和普通 BST 一样。
点击查看代码
namespace TREAP {class TreePoint {public:ll val, rk, sz, cnt;ll son[2];inline void NewP (ll x) { val = x, rk = rand (), cnt = sz = 1, son[0] = son[1] = 0;return; }};class Treap {public:TreePoint tr[N];ll tot = 0, rt = 0;#define va(p) tr[p].val#define rk(p) tr[p].rk#define sz(p) tr[p].sz#define cn(p) tr[p].cnt#define so(p, lr) tr[p].son[lr]inline void PushUp (ll p) { sz (p) = cn (p) + sz (so (p, 0)) + sz (so (p, 1)); return; }inline ll NewP (ll num) { tr[++tot].NewP (num); return tot; }inline void DelP (ll p) { va (p) = rk (p) = sz (p) = cn (p) = so (p, 0) = so (p, 1) = 0;return; }inline void Rotate (ll& p, ll sd) {ll q = so (p, sd ^ 1);so (p, sd ^ 1) = so (q, sd);so (q, sd) = p, p = q;PushUp (so (q, sd)), PushUp (q);return;}void Insert (ll& p, ll x) {if (!p) {p = NewP (x);return;}if (va (p) == x) ++cn (p);else {bool sd = (va (p) rk (p)) Rotate (p, sd ^ 1);}PushUp (p);return;}void Delete (ll& p, ll x) {if (!p) return;if (va (p) == x) {if (cn (p) == 1) {if (!so (p, 0) && !so (p, 1)) DelP (p), p = 0;else if (!so (p, 0) || !so (p, 1)) p = so (p, 0) + so (p, 1);else {ll sd = (rk (so (p, 1)) va (p))), x);PushUp (p);return;}ll GetRank (ll p, ll x) {if (!p) return 1;if (va (p) == x) return 1 + sz (so (p, 0));if (va (p) < x) return GetRank (so (p, 1), x) + sz (so (p, 0)) + cn (p);return GetRank (so (p, 0), x);}ll GetKth (ll p, ll x) {if (!p) return 0;if (x <= sz (so (p, 0))) return GetKth (so (p, 0), x);x -= sz (so (p, 0));if (x <= cn (p)) return va (p);x -= cn (p);return GetKth (so (p, 1), x);}ll Pre (ll x) { return GetKth (rt, GetRank (rt, x) - 1); }ll Next (ll x) { return GetKth (rt, GetRank (rt, x + 1)); }#undef va#undef rk#undef sz#undef cn#undef so};}FHQ_Treap
FHQ_Treap 依旧满足 Treap 的性质,但是操作方式很神奇!
FHQ_Treap 也被称为无旋 Treap,因为它的所有操作都没有恶心的旋转,只有分裂和合并两个基础操作!
分裂有两种方法:按权值裂和按排名裂。一般来说,只当平衡树的时候通常按权值裂,维护序列的时候按排名裂。具体怎么裂见代码和例题。
合并的时候要保证第一棵树的所有权值都比第二棵树小,注意合的过程中要保证 Treap 的性质。
为了方便写我没有写副本数。
然后就是六个操作了:
插入
按 \(x\) 裂成 \(a,b\) 两棵树,然后按 \(a,x,b\) 的顺序合起来
删除
这绝对是删除操作最简单的平衡树了!先按 \(x\) 裂成 \(a,b\) 两棵树,再把 \(a\) 按 \(x-1\) 裂成 \(a,c\) 两棵树,此时
查询排名为 \(k\) 的数
和普通 BST 一样。
查询 \(x\) 的排名
按 \(x-1\) 裂成 \(a,b\) 两棵树,\(a\) 的大小加一就是答案
查询 \(x\) 的前驱
按 \(x-1\) 裂成 \(a,b\) 两棵树,\(a\) 里的最大值
查询 \(x\) 的后继
按 \(x-1\) 裂成 \(a,b\) 两棵树,\(b\) 里的最小值
点击查看代码
namespace FHQ_TREAP {class TreeNode {public:ll val, rk, sz, son[2];inline void Add (ll num) { val = num, rk = rand (), sz = 1, son[0] = son[1] = 0; return; }};class FHQTreap {private:TreeNode tr[N];ll tot = 0, rt = 0, a, b, c;#define va(p) tr[p].val#define rk(p) tr[p].rk#define sz(p) tr[p].sz#define so(p, lr) tr[p].son[lr]inline ll NewP (ll num) { tr[++tot].Add (num); return tot; }inline void PushUp (ll p) { sz (p) = 1 + sz (so (p, 0)) + sz (so (p, 1)); return; }void Split (ll p, ll x, ll& l, ll& r) {if (!p) l = r = 0;else {if (va (p) <= x) l = p, Split (so (p, 1), x, so (p, 1), r);else r = p, Split (so (p, 0), x, l, so (p, 0));PushUp (p);}return;}inline ll Merge (ll l, ll r) {if (!l || !r) return l + r;if (rk (l) < rk (r)) {so (l, 1) = Merge (so (l, 1), r);PushUp (l);return l;}else {so (r, 0) = Merge (l, so (r, 0));PushUp (r);return r;}}public:inline void Insert (ll x) {Split (rt, x, a, b);rt = Merge (Merge (a, NewP (x)), b);return;}inline void Delete (ll x) {Split (rt, x, a, b);Split (a, x - 1, a, c);rt = Merge (Merge (a, Merge (so (c, 0), so (c, 1))), b);return;}inline ll GetRank (ll x) {Split (rt, x - 1, a, b);ll ans = sz (a) + 1;rt = Merge (a, b);return ans;}inline ll GetKth (ll x) {ll p = rt;while (p) {if (x <= sz (so (p, 0))) p = so (p, 0);else {x -= sz (so (p, 0)) + 1;if (!x) break;p = so (p, 1);}}return va (p);}inline ll Pre (ll x) {Split (rt, x - 1, a, b);ll p = a;while (so (p, 1)) p = so (p, 1);rt = Merge (a, b);return va (p);}inline ll Next (ll x) {Split (rt, x, a, b);ll p = b;while (so (p, 0)) p = so (p, 0);rt = Merge (a, b);return va (p);}#undef va#undef rk#undef sz#undef so};}树套树
用于维护单点修改和区间第 \(k\) 大,排名,前驱和后继的查询。
首先建立一棵线段树,每个节点单建一棵平衡树维护这个区间(线段树的每一层有 \(n\) 个节点,一共 \(\log_2n\) 层,因此只有 \(n\log_2n\) 个节点,不会 TLE/MLE)。
然后是如何维护五个操作:
- 单点修改:所有包含这个点的平衡树删除原来这个点的数,再插入新数。
- \(x\) 的区间排名:将在这个区间内的平衡树的 \(x\) 加起来。
- \(x\) 的区间第 \(k\) 大:使用二分,找到一个数的区间排名是 \(k\)。
- \(x\) 的区间前驱:这个区间内的所有平衡树中 \(x\) 的前驱最大值。
- \(x\) 的区间后继:这个区间内的所有平衡树中 \(x\) 的后继最小值。
点击查看代码
const ll N = 1e5 + 10, inf = 2147483647;namespace FHQ_TREAP {class TreeNode {public:ll val, rk, sz, son[2];inline void Add (ll num) noexcept { val = num, rk = rand (), sz = 1, son[0] = son[1] = 0; return; }} tr[N << 4];ll tot = 0, len = 0, free[N << 4];#define va(p) tr[p].val#define rk(p) tr[p].rk#define sz(p) tr[p].sz#define so(p, lr) tr[p].son[lr]class FHQTreap {private:ll rt = 0, a, b, c;inline void PushUp (ll p) noexcept { sz (p) = 1 + sz (so (p, 0)) + sz (so (p, 1)); }inline ll NewP (ll num) noexcept {ll p = len ? free[len--] : ++tot;tr[p].Add (num);return p;}inline void DelP (ll p) noexcept {va (p) = rk (p) = sz (p) = so (p, 0) = so (p, 1) = 0;free[++len] = p;return;}inline void Split (ll p, ll x, ll& l, ll& r) noexcept {if (!p) l = r = 0;else {if (va (p) rk (r)) {so (l, 1) = Merge (so (l, 1), r);PushUp (l);return l;}else {so (r, 0) = Merge (l, so (r, 0));PushUp (r);return r;}}public:inline void Insert (ll x) noexcept {Split (rt, x, a, b);rt = Merge (Merge (a, NewP (x)), b);return;}inline void Delete (ll x) noexcept {Split (rt, x, a, b);Split (a, x - 1, a, c);rt = Merge (Merge (a, Merge (so (c, 0), so (c, 1))), b);DelP (c);return;}inline ll GetRank (ll x) noexcept {Split (rt, x - 1, a, b);ll ans = sz (a);rt = Merge (a, b);return ans;}inline ll Pre (ll x) noexcept {Split (rt, x - 1, a, b);ll p = a;while (so (p, 1)) p = so (p, 1);rt = Merge (a, b);return va (p);}inline ll Next (ll x) noexcept {Split (rt, x, a, b);ll p = b;while (so (p, 0)) p = so (p, 0);rt = Merge (a, b);return va (p);}};#undef va#undef rk#undef sz#undef so}namespace SEGMENT_TREE {class SegmentTree {private:FHQ_TREAP::FHQTreap tr[N << 2];#define ls(p) p << 1, l, mid#define rs(p) p << 1 | 1, mid + 1, rpublic:inline void Build (ll p, ll l, ll r, ll* a) noexcept {if (l != r) {ll mid = md;Build (ls (p), a);Build (rs (p), a);}tr[p].Insert (inf), tr[p].Insert (-inf);_for (i, l, r) tr[p].Insert (a[i]);return;}inline void Update (ll p, ll l, ll r, ll x, ll y, ll z) noexcept {if (r < x || x < l) return;if (l != r) {ll mid = md;Update (ls (p), x, y, z);Update (rs (p), x, y, z);}tr[p].Delete (z), tr[p].Insert (y);}inline ll QueryRank (ll p, ll l, ll r, ll le, ll ri, ll x) noexcept {if (ri < l || r < le) return 0;ll mid = md;if (le <= l && r <= ri) return tr[p].GetRank (x) - 1;else return QueryRank (ls (p), le, ri, x) + QueryRank (rs (p), le, ri, x);}inline ll QueryKth (ll le, ll ri, ll x, ll n, ll mx) noexcept {ll l = 0, r = mx, ans = 0;while (l <= r) {ll mid = md;if (QueryRank (1, 1, n, le, ri, mid) + 1 <= x) ans = mid, l = mid + 1;else r = mid - 1;}return ans;}inline ll QueryPre (ll p, ll l, ll r, ll le, ll ri, ll x) noexcept {if (ri < l || r < le) return -inf;ll mid = md;if (le <= l && r <= ri) return tr[p].Pre (x);else return std::max (QueryPre (ls (p), le, ri, x), QueryPre (rs (p), le, ri, x));}inline ll QueryNext (ll p, ll l, ll r, ll le, ll ri, ll x) noexcept {if (ri < l || r < le) return inf;ll mid = md;if (le <= l && r <= ri) return tr[p].Next (x);else return std::min (QueryNext (ls (p), le, ri, x), QueryNext (rs (p), le, ri, x));}};}平衡树的区间操作
平衡树不是只能平衡树,也可以进行区间操作。
用平衡树中序遍历顺序不变的性质,维护序列中每个数的前后位置(即把按数值排序变为按下标排序)。
操作时,把需要操作/查询的区间放在一颗子树上再直接对子树进行操作/查询。
如果操作对子树的所有点生效,应该给子树打个标记,旋转/分裂/合并的时候随手下传标记。
具体的
使用 Splay:通过对 \(l-1\) 和 \(r+1\) 提根使得区间 \([l, r]\) 在一颗子树上,然后对这棵子树进行操作。
使用 FHQ-Treap:把区间 \([l, r]\) 裂出来,然后对这棵子树进行操作,再合并回去。
平衡树还支持插入/删除一个点,所以维护序列的时候还可以在任意位置加入/删除一个数。
另外,FHQ-Treap 裂开合并的神奇操作还支持对一个区间进行移动。
例题P3391 文艺平衡树思路
对需要操作的区间打个翻转标记,同时交换其左右儿子。
P4036 [JSOI2008]火星人思路
维护一棵子树的字符串的哈希值,然后就是裸的区间操作了。
P4309 [TJOI2013]最长上升子序列思路
不难发现每次插入的数都会比之前插入的数都大,因此插完之后最长上升子序列的长度不会变化。
那么每个节点维护一个子树最长上升子序列的长度的最大值,插入时选一个前面的最长的最长上升子序列接上。
星系探索思路
把这棵树转换成 dfs 序序列,然后对于三个操作:
- 求 \(u\) 到根的权值和:求 \(u\) 在 dfs 序序列上的前缀和。
- 改变 \(u\) 的父亲:移动 \(u\) 子树的 dfs 序序列代表的区间的位置。
- 给 \(u\) 子树加一个定值:把 \(u\) 子树的 dfs 序序列代表的区间裂出来,打个标记再合并回去。
代码
点击查看代码
const ll N = 1e6+ 10;namespace FHQ_TREAP {class TreeNode {public:ll val, pn, rk, sz, so[2], ta, sum, sp, fa;inline void Add (ll num, ll tmp) { sum = val = num * tmp, sp = pn = tmp, rk = rand (), sz = 1, so[0] = so[1] = 0; return; }};class FHQTreap {private:TreeNode tr[N];ll tot = 0, rt = 0, a, b, c;#define va(p) tr[p].val#define ta(p) tr[p].ta#define rk(p) tr[p].rk#define sz(p) tr[p].sz#define pn(p) tr[p].pn#define su(p) tr[p].sum#define sp(p) tr[p].sp#define fa(p) tr[p].fa#define so(p, lr) tr[p].so[lr]inline ll NewP (ll num, ll pn) { tr[++tot].Add (num, pn); return tot; }inline void PushUp (ll p) {sz (p) = 1 + sz (so (p, 0)) + sz (so (p, 1));su (p) = va (p) + su (so (p, 0)) + su (so (p, 1));sp (p) = pn (p) + sp (so (p, 0)) + sp (so (p, 1));fa (so (p, 0)) = fa (so (p, 1)) = p;return;}inline void Tag (ll p, ll num) {ta (p) += num;va (p) += num * pn (p);su (p) += num * sp (p);return;}inline void PushDown (ll p) {if (!ta (p)) return;if (so (p, 0)) Tag (so (p, 0), ta (p));if (so (p, 1)) Tag (so (p, 1), ta (p));fa (so (p, 0)) = fa (so (p, 1)) = p;ta (p) = 0;return;}inline void Split (ll p, ll x, ll& l, ll& r) {if (!p) l = r = 0;else {PushDown (p);if (sz (so (p, 0)) rk (r)) {so (l, 1) = Merge (so (l, 1), r);PushUp (l);return l;}else {so (r, 0) = Merge (l, so (r, 0));PushUp (r);return r;}}inline ll GetRank (ll x) {ll cnt = sz (so (x, 0)) + 1;for (ll p = x; fa (p); p = fa (p))if (so (fa (p), 1) == p) cnt += sz (so (fa (p), 0)) + 1;return cnt;}public:inline void Insert (ll x, ll p) {rt = Merge (rt, NewP (x, p));return;}inline void Modify (ll l, ll r, ll x) {l = GetRank (l), r = GetRank (r);Split (rt, r, a, b);Split (a, l - 1, a, c);Tag (c, x);rt = Merge (Merge (a, c), b);return;}inline void Move (ll l, ll r, ll x) {l = GetRank (l), r = GetRank (r), x = GetRank (x);if (x > r) x -= r - l + 1;Split (rt, r, a, b);Split (a, l - 1, a, c);a = Merge (a, b);Split (a, x, a, b);rt = Merge (Merge (a, c), b);return;}inline ll Query (ll x) {x = GetRank (x);Split (rt, x, a, b);ll ans = su (a);rt = Merge (a, b);return ans;}#undef va #undef ta#undef rk#undef sz#undef pn#undef su#undef sp#undef fa#undef so};}namespace SOLVE {FHQ_TREAP::FHQTreap tr;ll n, m, fa[N], w[N], cnt;ll dfn[N], sec[N][2];std::vector tu[N];inline ll rnt () {ll x = 0, w = 1; char c = getchar ();while (!isdigit (c)) { if (c == '-') w = -1; c = getchar (); }while (isdigit (c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar ();return x * w;}inline char rch () {char c = getchar ();while (c < 'A' || 'Z' < c) c = getchar ();return c;}inline void Dfs (ll x) {dfn[sec[x][0] = ++cnt] = x;tr.Insert (w[x], 1);far (i, tu[x]) Dfs (i);sec[x][1] = ++cnt;tr.Insert (w[x], -1);return;}inline void In () {n = rnt ();_for (i, 2, n) {fa[i] = rnt ();tu[fa[i]].push_back (i);}_for (i, 1, n) w[i] = rnt ();m = rnt ();Dfs (1);return;}inline void Out () {while (m--) {char opt = rch ();if (opt == 'Q') {ll d = rnt ();printf ("%lld\n", tr.Query (sec[d][0]));}else if (opt == 'C') {ll x = rnt (), y = rnt ();tr.Move (sec[x][0], sec[x][1], sec[y][0]);}else {ll x = rnt (), y = rnt ();tr.Modify (sec[x][0], sec[x][1], y);}}return;}}\[\Huge\mathfrak{The End}\]
本文来自博客园,作者:Keven-He,转载请注明原文链接:https://www.cnblogs.com/Keven-He/p/SplayAndTreap.html