特殊矩阵的压缩存储
矩阵:一个由m x n 个元素排列成的m列n行的表。
矩阵的常规存储的特点:
- 可以对其元素进行随机存储;
- 矩阵运算非常简单;存储密度为1;
不适宜常规存储的矩阵:值相同的元素很多且呈某种规律分布;零元素多。
矩阵的压缩存储:为多个相同的非零元素只分配一个存储;对零元素不分配空间。
- 什么是压缩存储?
若多个数据元素的值都相同,则只分配一个元素值的存储空间,且零元素不占存储空间。 - 什么样的矩阵能够压缩?
一些特殊矩阵,如:对称矩阵,对角矩阵,三角矩阵,稀疏矩阵等。 - 什么叫稀疏矩阵?
矩阵中非零元素的个数较少(一般小于5%)
对称矩阵
【特点】在n x n矩阵a中,满足如下性质:
aij = aji (1 <= i , j <= n)
【存储方法】只存储下(或者上)三角(包括主对角线)的数据元素。共占用 n(n+1)/2个元素空间。
【存储结构】:对称矩阵上下三角中的元素均为n(n+1)/2,可以以行序为主序将元素存放在一个一维数组sa[n(n+1)/2]中。
aij为第i(i-1)/2-1+j个元素
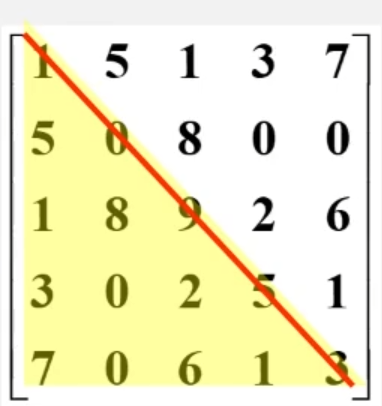
三角矩阵
【特点】对角线以下(或者以上)的元素数据(不包括对角线)全部为常数c;
【存储方法】重复元素c共享一个元素存储空间,共占用n( n + 1 ) / 2 + 1个元素,空间:sa[1 … n(n+1)/2+1],矩阵下标还是从1开始。
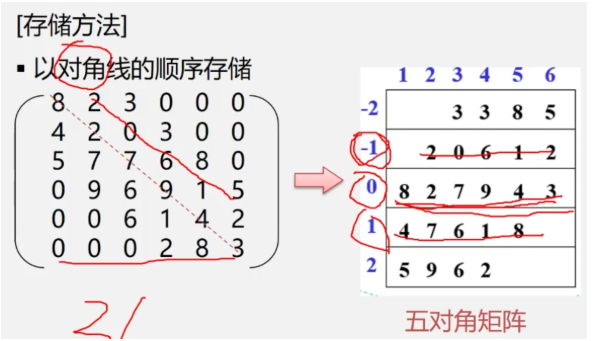
对角矩阵(带状矩阵)
【特点】在n x n的方阵中,所有非零元素都集中在以主对角线为中心的带状区域中,区域外的值全为0,则称为对角矩阵。常见的有三对角矩阵、五对角矩阵、七对角矩阵等。
【存储方法】