✨作者：@平凡的人1
✨专栏：《小菜鸟爱刷题》
✨一句话：凡是过往，皆为序章
✨说明: 过去无可挽回，未来可以改变

为了方便自己的学习以及基于好久没更新博客的原因。特地写了这一篇博客。
本篇博客是一篇记录学习篇，我将之归纳于刷题专栏。方便自己的复习以及分享一些自己的学习过程。
如果你觉得有错误的地方，一定要及时地告诉我哦，毕竟博主能力有限，请多多指教呀

下面我们进入今天的主题

文章目录

Leetcode简单题
- 258.各位相加
- 263.丑数
- 283.移动0
- 326.3的幂
- 367.有效的完全平方数
- 374.猜数字大小
- 414.第三大的数
- 509.斐波那契数
- 520.检测大写字母
- 1295.统计位数为偶数的数字
- 1346.检查整除及其两倍数是否存在
数据结构基础选填题
- 选择题
- 填空题
总结

Leetcode简单题

258.各位相加

给定一个非负整数 num，反复将各个位上的数字相加，直到结果为一位数。返回这个结果。
示例 1:
输入: num = 38
输出: 2
解释: 各位相加的过程为：
38 –> 3 + 8 –> 11
11 –> 1 + 1 –> 2
由于 2 是一位数，所以返回 2。
示例 1:
输入: num = 0
输出: 0
提示：
0 <= num <= 231 – 1
来源：力扣（LeetCode）

我们可以先想一想：如果一个数是小于10的话，那就直接返回即可。当大于10时候：比如例子中的38，把各位求出来相加之后还是大于10的，我们还是要继续重复求出各个位，知道相加是小于10的这个过程。

解题思路：基于此，我们可以通过两层循环：里面一层可以用来计算第一次的各位相加之和，外面一层在来计算所得和如果大于10的过程。知道算出最终的结果。下面实现代码：

这里要注意的就是第一次算完之后sum要重置为0，在继续算下去，下面进行提交运行：

263.丑数

丑数就是只包含质因数 2、3 和 5 的正整数。
给你一个整数 n ，请你判断 n 是否为丑数。如果是，返回 true ；否则，返回 false 。
示例 1：
输入：n = 6
输出：true
解释：6 = 2 × 3
示例 2：
输入：n = 1
输出：true
解释：1 没有质因数，因此它的全部质因数是 {2, 3, 5} 的空集。习惯上将其视作第一个丑数。
示例 3：
输入：n = 14
输出：false
解释：14 不是丑数，因为它包含了另外一个质因数 7 。
来源：力扣（LeetCode）

直接去判断这个数是否能够整除质因数2、3、5，能够整除的话，继续让这个数除以对应的质因数，知道最后，判断是否能够等于1，等于1的话就是丑数，不等的话就不是丑数。比如例子中的6，能够整除2，继续除以2等于4，又能够整除2，继续除以2，又能够整除2，最终得到结果1。下面实现并提交运行代码：

283.移动0

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。
请注意，必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
来源：力扣（LeetCode）

解题思路：第一次去遍历数组中不等于0的数，放在数组中，第二次去遍历：从第一次遍历完成的下标开始，直接让后面（小于数组的长度）的数等于0即可完成题目的要求。下面实现并提交代码：

不过这种做法感觉效率太低了一点 不过我就是这么菜

326.3的幂

给定一个整数，写一个函数来判断它是否是 3 的幂次方。如果是，返回 true ；否则，返回 false 。
整数 n 是 3 的幂次方需满足：存在整数 x 使得 n == 3x
示例 1：
输入：n = 27
输出：true
示例 2：
输入：n = 0
输出：false
示例 3：
输入：n = 9
输出：true
示例 4：
输入：n = 45
输出：false
来源：力扣（LeetCode）

感觉这种题真的有一种规律，就像上面263.丑数的思路一样，如果能够整除3的话，那就让这个数继续去除以3,最后再去判断是否等于1即可。由此类推，4的幂也不难求解。下面实现代码及提交运行代码：

367.有效的完全平方数

给定一个正整数 num ，编写一个函数，如果 num 是一个完全平方数，则返回 true ，否则返回 false 。
进阶：不要使用任何内置的库函数，如 sqrt 。
示例 1：
输入：num = 16
输出：true
示例 2：
输入：num = 14
输出：false
来源：力扣（LeetCode）

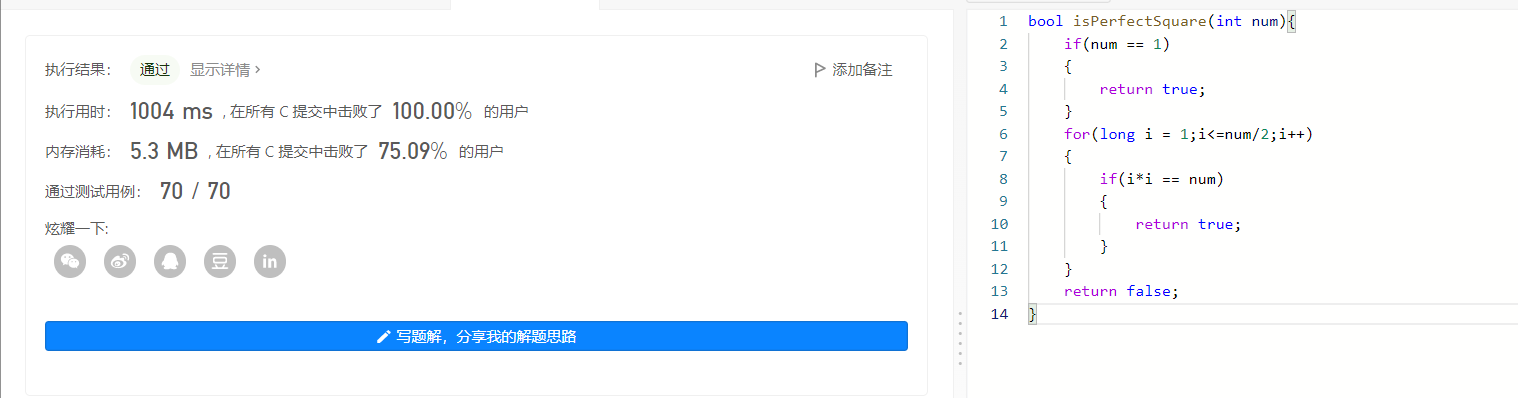
字面意思，直接for循环走起来即可，同时要注意到变量的类型，防止溢出

下面进行实现代码，提交运行：

374.猜数字大小

猜数字游戏的规则如下：
每轮游戏，我都会从 1 到 n 随机选择一个数字。请你猜选出的是哪个数字。
如果你猜错了，我会告诉你，你猜测的数字比我选出的数字是大了还是小了。
你可以通过调用一个预先定义好的接口 int guess(int num) 来获取猜测结果，返回值一共有 3 种可能的情况（-1，1 或 0）：
-1：我选出的数字比你猜的数字小 pick < num
1：我选出的数字比你猜的数字大 pick > num
0：我选出的数字和你猜的数字一样。恭喜！你猜对了！pick == num
返回我选出的数字。
示例 1：
输入：n = 10, pick = 6
输出：6
示例 2：
输入：n = 1, pick = 1
输出：1
示例 3：
输入：n = 2, pick = 1
输出：1
示例 4：
输入：n = 2, pick = 2
输出：2
来源：力扣（LeetCode）

刚开始一直看不懂题目在说啥（好吧，没认真看题目）。

就是已经提供了一个函数接口guess（int num）然后我们去判断大小，这其实就是在找一个数，我们可以用二分查找的思想来解决这个题目，不说了，直接实现。下面实现代码并提交运行：

414.第三大的数

给你一个非空数组，返回此数组中第三大的数。如果不存在，则返回数组中最大的数。
示例 1：
输入：[3, 2, 1]
输出：1
解释：第三大的数是 1 。
示例 2：
输入：[1, 2]
输出：2
解释：第三大的数不存在, 所以返回最大的数 2 。
示例 3：
输入：[2, 2, 3, 1]
输出：1
解释：注意，要求返回第三大的数，是指在所有不同数字中排第三大的数。
此例中存在两个值为 2 的数，它们都排第二。在所有不同数字中排第三大的数为 1 。
来源：力扣（LeetCode）

==直接从大到小排序，然后输出第三个数即可？？？==❌

因为数组中可能含有相同的数字，这就需要我们去处理一下了：排序完之后，我们可以定义一个计算器，如果不相邻的话，让count++，知道count==3即可输出：

提交运行代码：

509.斐波那契数

斐波那契数（通常用 F(n) 表示）形成的序列称为斐波那契数列。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：
F(0) = 0，F(1) = 1
F(n) = F(n – 1) + F(n – 2)，其中 n > 1
给定 n ，请计算 F(n) 。
来源：力扣（LeetCode）

无需多言，直接实现：

520.检测大写字母

我们定义，在以下情况时，单词的大写用法是正确的：
全部字母都是大写，比如 “USA” 。
单词中所有字母都不是大写，比如 “leetcode” 。
如果单词不只含有一个字母，只有首字母大写，比如 “Google” 。
给你一个字符串 word 。如果大写用法正确，返回 true ；否则，返回 false 。
示例 1：
输入：word = “USA”
输出：true
示例 2：
输入：word = “FlaG”
输出：false
来源：力扣（LeetCode）

那就把三种情况罗列出来不就行了：

不过我们需要借助一个计算器count，if（全部大写count== strlen(word) || 全部都不是大写count == 0 || 只有一个大写，且在首位置count == 1&& word>=‘A’&&word<=‘Z’）

实现代码并提交运行：

1295.统计位数为偶数的数字

给你一个整数数组 nums，请你返回其中位数为偶数的数字的个数。
示例 1：
输入：nums = [12,345,2,6,7896]
输出：2
解释：
12 是 2 位数字（位数为偶数）
345 是 3 位数字（位数为奇数）
2 是 1 位数字（位数为奇数）
6 是 1 位数字位数为奇数）
7896 是 4 位数字（位数为偶数）
因此只有 12 和 7896 是位数为偶数的数字
示例 2：
输入：nums = [555,901,482,1771]
输出：1
解释：
只有 1771 是位数为偶数的数字。
来源：力扣（LeetCode）

首先去实现一个函数判断一个数的位数是否为偶数，然后去遍历整个数组，如果是偶数的话加起来就行了：

提交运行：

1346.检查整除及其两倍数是否存在

给你一个整数数组 arr，请你检查是否存在两个整数 N 和 M，满足 N 是 M 的两倍（即，N = 2 * M）。
更正式地，检查是否存在两个下标 i 和 j 满足：
i != j
0 <= i, j < arr.length
arr[i] == 2 * arr[j]
示例 1：
输入：arr = [10,2,5,3]
输出：true
解释：N = 10 是 M = 5 的两倍，即 10 = 2 * 5 。
示例 2：
输入：arr = [7,1,14,11]
输出：true
解释：N = 14 是 M = 7 的两倍，即 14 = 2 * 7 。
示例 3：
输入：arr = [3,1,7,11]
输出：false
解释：在该情况下不存在 N 和 M 满足 N = 2 * M 。
来源：力扣（LeetCode）