作者主页：

二叉树顺序存储在 物理 上是一个 数组，在 逻辑 上是一棵 二叉树。

我们这篇博客学习的堆就是使用 顺序存储 来实现。

二、堆的概念和结构

概念：如果有一个关键码的集合 K = {k0 ， k1 ， k2 ， … ， kn-1} ，把它的所有元素按完全二叉树的顺序存储方式存储在一 个一维数组中 ，并满足： Ki <= K2i+1 且 Ki= K2i+1 且 Ki >=K2i+2) i = 0 ， 1 ， 2… ，则称为小堆 ( 或大堆) 。（即双亲比孩子的数值小(大)——小(大)堆）将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

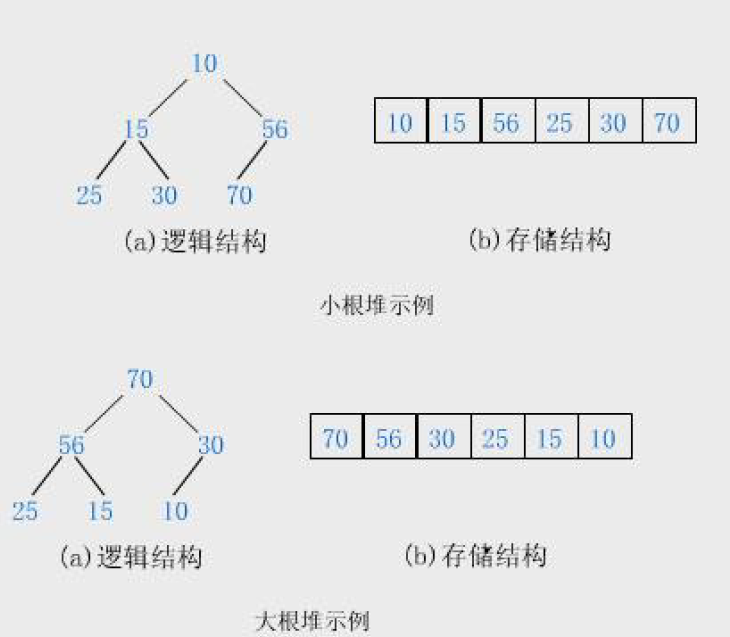
堆分为 大堆 和 小堆 ：

• 大堆：树中所有父亲节点数据大于等于孩子节点数据
• 小堆：树中所有父亲节点数据小于等于孩子节点数据

堆的性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值
• 堆是一棵完全二叉树

说了这么多，其实判断是否为堆最好的方式就是 画图，画出堆构成的完全二叉树，看其是否符合性质。

三、堆的实现

实现堆之前，我们需要了解一下概念：左孩子下标为奇数，右孩子下标为偶数

根据概念推导：

左孩子下标 = 2 * 双亲下标 + 1

右孩子下标 = 2 * 双亲下标 + 2

双亲下标 = (孩子下标 – 1) / 2 —— 这个式子是向下取整的，左右孩子都适用

1、结构的定义

堆是完全二叉树，其存储结构是顺序存储。那就和顺序表一样，将数据存在数组中，给定size 记录堆中元素个数，capacity 记录堆的最大容量。

typedef int HPDataType;typedef struct Heap{HPDataType* a; // 存储数据的空间int size; // 大小int capacity; // 容量}HP;

本篇博客默认实现的是 小堆。

2、接口总览

void HeapPrint(HP* php); // 打印void HeapInit(HP* php); // 初始化void HeapDestroy(HP* php); // 销毁void HeapPush(HP* php, HPDataType x); // 堆尾插入数据void HeapPop(HP* php); // 删除堆顶数据HPDataType HeapTop(HP* php); // 取堆顶数据int HeapSize(HP* hp); // 计算大小bool HeapEmpty(HP* hp); // 判空void AdjustUp(HPDataType* a, int child); // 向上调整void AdjustDown(HPDataType* a, int n, int parent); // 向下调整

3、初始化

堆的初始化和顺序表是一样的，因为我们用的就是顺序存储：

void HeapInit(HP* php){assert(php);php->a = NULL;php->size = php->capacity = 0;}

4、销毁

堆的销毁只要释放空间，然后把 size 和 capacity 置0就可以。

void HeapDestroy(HP* php){assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;}

5、插入

堆的插入就是在 数组尾部 的插入，就是 数组 的 尾插。

堆插入数据只会在尾部，所以无需封装接口用来扩容，直接判断是否要扩容就可以。

堆在插入数据后，需要保持堆的结构，之前是小/大堆，在插入数据后也应该是小/大堆。当插入数据后，如果破坏了结构，就需要 向上调整。

void HeapPush(HP* php, HPDataType x){assert(php);// 检查容量if (php->size == php->capacity){int newcapacity = php->capacity == 0 " />
 
插入数据 小于 它的 祖先(从根到该节点所经分支上的所有节点，就是它的父亲，爷爷等)，插入后，不为小堆，此时需要将 插入数据需要向上调整，直到它为小堆：
 
 
理清了这两个情况，再梳理一下细节：
 
向上调整，肯定是以 孩子为基准，孩子调整到堆顶就代表着向上调整结束了。如果使用父亲为基准的话，是非正常结束的(孩子调整到0没有结束，而是通过比较值后，break退出的)。
 
而中间的过程就是判断孩子是否小于父亲，如果小于就交换它们的值，然后将孩子迭代为父亲，再重新计算父亲，继续调整上方；如果孩子大于等于父亲，就退出，无需调整。
 
通过不断向上调整元素，就可以构建出来 小堆。
 
void Swap(HPDataType* p1, HPDataType* p2){assert(p1 && p2);HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;}void AdjustUp(HPDataType* a, int child){assert(a);// 求父亲int parent = (child - 1) / 2;// 默认小堆while (child > 0){        // 如果孩子小于父亲，调整if (a[child] < a[parent]){Swap(&a[child], &a[parent]); // 交换child = parent; // 孩子迭代为父亲parent = (child - 1) / 2; // 重新计算父亲}else{break;}}}
建大堆 只要修改一下条件：
if (a[child]) > a[parent]
7、删除
堆的 删除 为删除 堆顶的数据。
对于删除来说，有两个方案：
直接头删
交换 堆顶 和 堆底 元素，尾删堆底元素，将堆顶元素 向下调整。(堆底元素就是数组尾部的元素)。
我们先看看 方案一 可不可行：
首先，由于堆是顺序存储的，那么 头删就要挪动数据，时间复杂度就为O(N)。其次，这样会 完全打乱关系。
举个例子，假设 15 和 18 在第二层原本是兄弟，但是由于头删，15到了堆顶，变成了 18 的父亲。关系就乱了，感情也就淡了(doge)。18 表示 我拿你当兄弟，你却想当我父亲。但是就这一对的话，还能忍忍，但是全部的父子关系都被破坏了，所以肯定不可行。
所以，方案一就被否决了，那就只能使用 方案二 了：
方案二的话就很好，删除元素前，交换了堆顶和堆底的元素，然后将堆底尾删，尾删的时间复杂度只有O(1)。通过向下调整对堆顶元素 下调 时，也不会破坏过多的关系。
void HeapPop(HP* php){assert(php);assert(php->size > 0); // 堆空不能删// 交换堆顶和最后一个节点的值Swap(&php->a[0], &php->a[php->size - 1]);// 尾删php->size--;AdjustDown(php->a, php->size, 0); // 向下调整}
8、向下调整
向下调整的步骤为：
找到左右孩子中的 小孩子。
判断 父亲 是否大于 小孩子，如果是则交换，不是则退出
交换后将 父亲迭代到大孩子的位置，重新计算孩子。
注意找最大孩子的时候，大孩子必须存在，小心越界。
向下调整的 循环条件 为 孩子下标 < 堆的大小，如果继续调整就越界了。
void Swap(HPDataType* p1, HPDataType* p2){assert(p1 && p2);HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;}void AdjustDown(HPDataType* a, int n, int parent){// 假设最小孩子int minchild = 2 * parent + 1;while (minchild < n){// 找最小孩子if (minchild + 1 < n && a[minchild + 1] < a[minchild]){minchild++;}        // 如果父亲大于孩子，调整if (a[parent] > a[minchild]){Swap(&a[parent], &a[minchild]); // 交换parent = minchild; // 迭代minchild = 2 * parent + 1;}else{break;}}}
调大堆 只要改变两个条件：
if (minchild + 1 < n && a[minchild + 1] > a[minchild]) // 找大孩子if (a[parent] < a[minchild]) // 如果父亲小于孩子，则交换
9、取堆顶数据
若堆非空，则取0下标位置数据：
HPDataType HeapTop(HP* php){assert(php);assert(php->size > 0);return php->a[0];}
10、计算堆大小
这就更简单了，直接返回 size：
int HeapSize(HP* php){assert(php);return php->size;}
11、判空
只要 size == 0 ，堆就为空：
bool HeapEmpty(HP* php){assert(php);return php->size == 0;}
12、打印堆
void HeapPrint(HP* php){assert(php);for (int i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");}
四、完整代码
Heap.h
#pragma once#include #include #include #include typedef int HPDataType;typedef struct Heap{HPDataType* a;int size;int capacity;}HP;// 堆的构建void HeapCreate(HP* hp, HPDataType* a, int n);void HeapPrint(HP* php);void HeapInit(HP* php);void HeapDestroy(HP* php);// 保持他继续是一个堆 O(logN)void HeapPush(HP* php, HPDataType x);// 删除堆顶的数据，并且保持他继续是一个堆 O(logN)void HeapPop(HP* php);HPDataType HeapTop(HP* php);int HeapSize(HP* hp);// 堆的判空bool HeapEmpty(HP* hp);
Heap.c
 
#define _CRT_SECURE_NO_WARNINGS 1 #include "Heap.h"void HeapPrint(HP* php){assert(php);for (int i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");}// 初始化 不开空间void HeapInit(HP* php){assert(php);php->a = NULL;php->size = php->capacity = 0;}// 销毁void HeapDestroy(HP* php){assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;}void Swap(HPDataType* p1, HPDataType* p2){assert(p1 && p2);HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;}// 向上调整void AdjustUp(HPDataType* a, int child){assert(a);// 算父亲int parent = (child - 1) / 2;// 默认小堆while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}// 保持他继续是一个堆 O(logN)void HeapPush(HP* php, HPDataType x){assert(php);// 检查容量if (php->size == php->capacity){int newcapacity = php->capacity == 0 " />