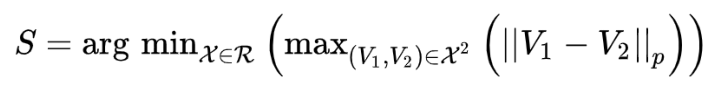论文链接:http://proceedings.mlr.press/v80/mhamdi18a/mhamdi18a.pdf
SGD存在问题
数据并行的SGD梯度聚合是所有梯度的线性组合,即:
\(F(G_1, …, G_n) = \sum_{i=1}^n\lambda_iG_i\)
因此一个恶意的节点可以让全局模型朝着自己想的方向偏移(\(G_n\)为恶意节点的梯度):
\(G_n = \dfrac{1}{\lambda_n}(U – \sum_{i=1}^{N-1}\lambda_iG_i)\)
如图所示: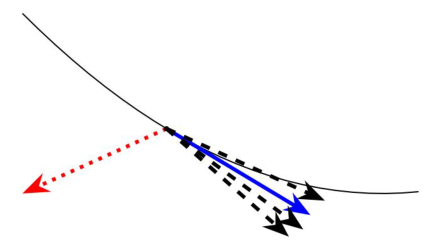
由此,我们需要新的梯度聚合规则(GAR)
\((\alpha, f)\)-Byzatine Resilient GAR定义
\((\alpha, f)\)解释:包含\(f\)个拜占庭梯度;\(\alpha\)为角度
如果某算法为\((\alpha, f)\)-Byzatine Resilient算法,则满足以下规则:
- 输出的梯度为一个与正确的梯度\(g\)相差最多为\(\alpha\)的梯度
- 输出的梯度为被正确的梯度\(g\)的矩所约束的梯度

现有\((\alpha, f)\)-Byzatine Resilient GAR举例:Krum, Multi-Krum, Brute等。
Krum算法介绍
要求:n ≥ 2f + 3
算法步骤:
- 计算节点i的梯度与其余节点j(邻居节点)的梯度的距离(欧氏距离)
- 选取距离自己最近的n-f-2个梯度,然后将选取的梯度求和,作为节点i的得分score
- 得分最小的节点的梯度即为算法输出的梯度
Brute算法介绍
要求:n ≥ 2f + 1
算法步骤:
- 列出所有可能的簇(每个簇中包含n – f个节点)
- 找到最紧密相连的簇(该簇中距离最远的梯度是所有的簇中距离最近的):

- 将找到的簇中的节点的梯度取平均
GARs缺陷
模型参数包含远大于1的维度,由此\(L_p\)范数较难辨别出以下两种恶意攻击:
- 每个维度上的微小变化
- 单一维度上的巨大变化
这样就较难收敛到一个较好的模型
Bulyan算法
要求:n ≥ 4f + 3
- 选出\(\theta\) = 2\(f\) + 3个梯度(根据Krum或Brute等算法选)
- 对梯度的每一维都选出\(\beta\) = \(\theta\) – 2\(f\) ≥ 3个值,这些值是距离每一维梯度的中位数最近的值
- 计算均值
结果

可以看出来在使用norm 2攻击的情况下,Bulyan准确率与没有攻击下的Average聚合算法的准确率大致相同。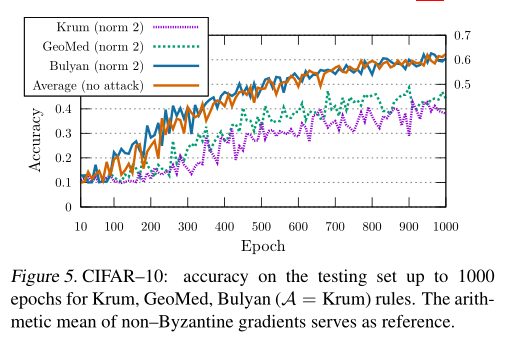
Bulyan优点
- 相较于其它算法(Krum、GeoMed)代价较小,平均计算复杂度为\(O((n-2f)C+dn)\)
- 该算法可以在每个维度上工作,即可以识别出某一个变化很大的维度(克服了Krum算法的缺陷)。之所以可以工作在每一个维度上,是因为Bulyan结合了例如Trimbed Mean的算法,处理了每一个维度。