对CART决策树剪枝过程的理解
前言:CART决策树生成的过程比较好理解,但是剪枝的过程看了好几遍才看明白,故写出下文,供同样困惑的朋友参考。下文不涉及复杂严密的数学推导,以辅助理解为主。
一. 损失函数的定义方法
CART的损失函数用的是下式:
\[C_\alpha(T)=C(T)+\alpha |T| \tag{1}\]
损失函数表征的是模型预测错误的程度,所以它越小越好。
上式中\(C_\alpha (T)\) 是关于 \(T\) 和 \(\alpha\) 的函数,\(T\) 表示一个决策树,\(C(T)\) 是对训练数据的预测误差(分类用基尼指数表示,回归用均方误差表示),\(|T|\) 表示树 \(T\) 的叶节点个数。$\alpha $ 是一个常数,用来平衡模型对数据的拟合程度(由\(C(T)\)项决定)和 模型的复杂度(\(\alpha|T|\)项决定,复杂度也就是树的分支多不多)。
如果 \(\alpha\) 非常小,那么损失函数 \(C_\alpha(T)\) 的值大小由 \(C(T)\) 决定,为了使损失函数的值小,\(C(T)\) 也就会趋于小,也就是多分枝,充分延展树(因为我们生成树时,选择属性的标准就是使基尼指数或者均方误差减小的最多,所以充分分枝意味着更小的 \(C(T)\));
反之,如果 \(\alpha\) 充分大,那么损失函数 \(C_\alpha(T)\) 的值大小由 \(\alpha |T|\) 决定,为了使损失函数的值小, \(|T|\) 也就会趋于小,而最小的树就是只有一个节点,所以此时剪枝成一个单节点树,\(|T|=1\) 。
总而言之,\(\alpha\) 越大,在损失函数的影响下,模型趋向于少分枝。\(\alpha\)越小,模型越趋向于多分枝。
二. 剪枝的过程
假设通过CART生成一个完整的树\(T_0\),如下:
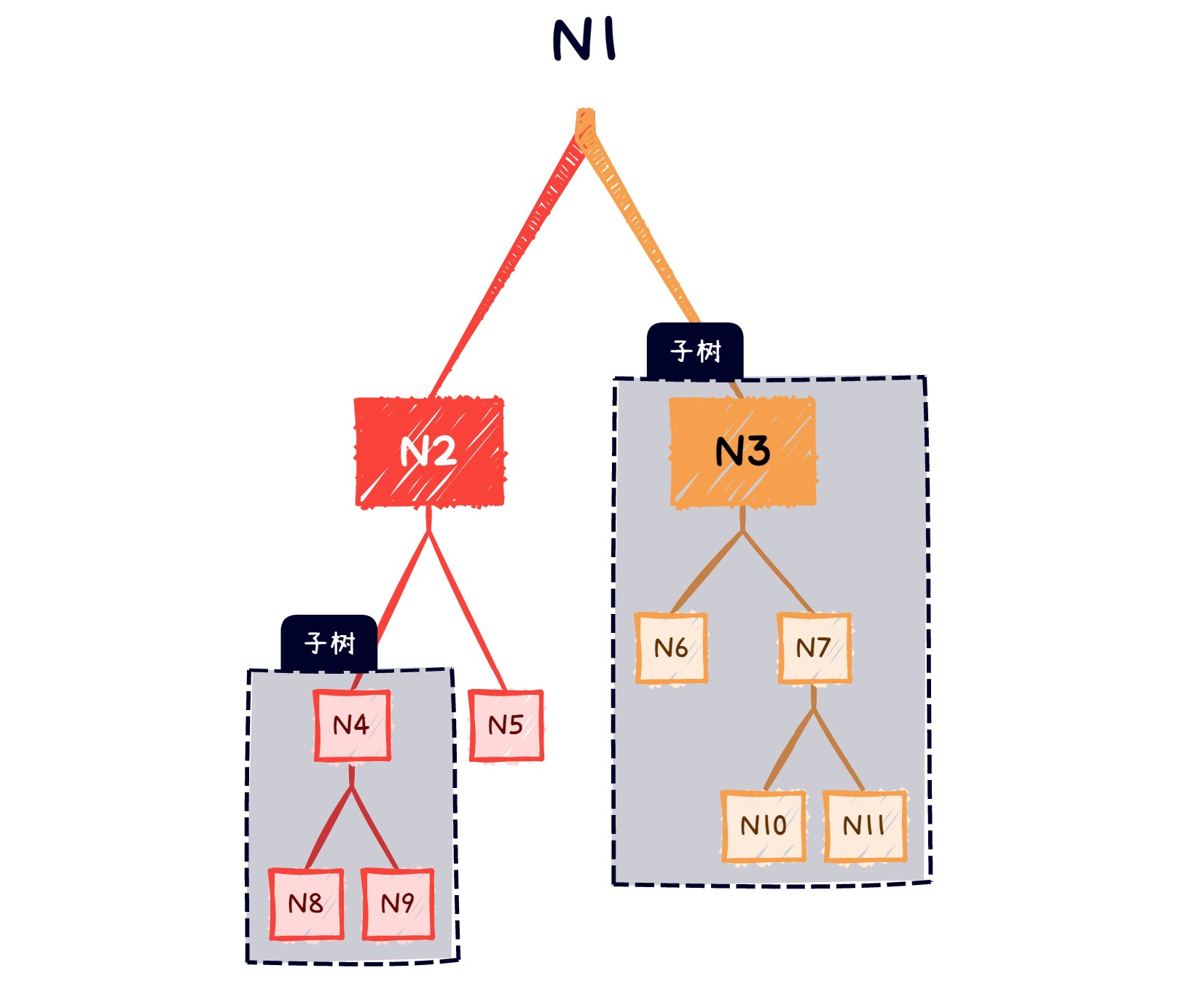
剪枝的整体思路是:
每次树所有的內结点(不是叶结点的结点,如上示树的N4,N2,N3,N7,N1),得出最适合剪枝的结点并对其剪枝,得到一个子树 \(T_i\) ,然后再分析 \(T_i\) 的所有內结点,找出 \(T_i\) 最适合剪枝的结点并对其剪枝,得到子树 \(T_{i+1}\);
\(\cdots\)
重复至最终得到的子树只剩下三个结点(一个根结点连着两个叶结点),如果这个过程中,我们得到了 k+1 个子树(注意,每次剪完枝得到的子树都要存储起来),不妨记作 {\(T_0,T_1,\cdots,T_k\)};
最后使用交叉验证,看看哪个树的性能最好,我们就选择哪个树。
核心步骤是第一步,以下给出具体解释和方法:
第一部分我们分析过:\(\alpha\) 越大,越趋向于多分枝;\(\alpha\) 越小,越趋向于少分枝。所以,必定存在一个\(\alpha\),使得分不分枝都可以(分枝与不分枝的损失函数值相同),我们记这个\(\alpha\) 为 \(\alpha_0\)。所以,我们只需要依次将树的內结点和它的子节点组成的子树拿出来(比如上示树中标示出来的以 \(N3\) 为根节点和以 \(N4\) 为根节点的子树),计算它的 \(\alpha_0\) 。对于全部的內结点,我们得到一组 \(\alpha_0\) 值,然后选择其中最小的 \(\alpha_0\) 对应內结点,并对其剪枝。
这句话需要稍微转个弯才能理解,为什么要选择 \(\alpha_0\) 最小的结点剪枝呢?假设我们选择了一个大于 \(min(\alpha_0)\) 的值 \(\alpha’\) 作为阈值,那么对于 剪枝阈值α0 小于 α′ 的结点,他们都处于 “趋向于不分枝“ 的状态,也就是需要剪枝,这样就会有多个结点需要剪枝,但是我们不能确保这些需要被剪枝的结点都是不相关的(剪掉一个后对另一个结点没有影响),所以我们需要控制每次只剪一个结点的枝,选择最小的\(\alpha_0\)对应的结点剪枝,就是为了控制每次只剪掉一个结点的枝,因为在损失函数是\(C_\alpha(T)=C(T)+\alpha_0 |T|\)的情况下,其他结点都处于 ”趋向于多分枝的状态“ 。
Breiman对此有严密的数学证明,感兴趣可以看看。
接下来就是确认每个內结点的\(\alpha_0\),注意,确认每个內结点的\(\alpha_0\)需要将该结点作为根节点的子树单独拿出来研究,以 \(N4\) 结点为例,首先我们把它作为根节点的子树拿出来:
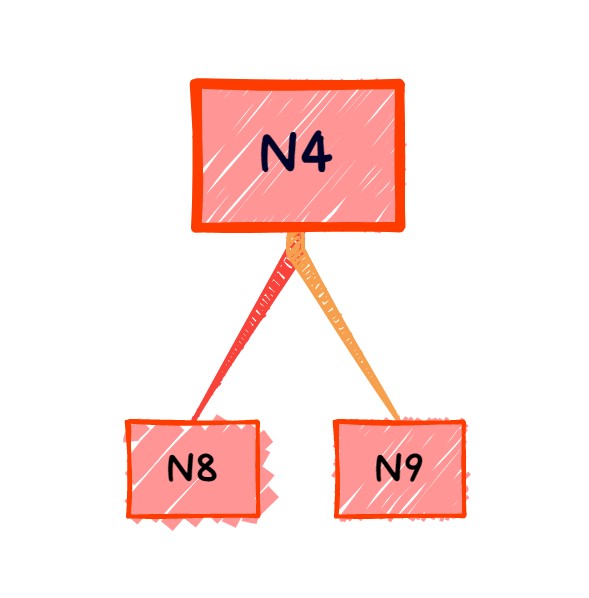
不剪枝,它的损失函数是:
\[C_\alpha(T_{N4})=C(T_{N4})+\alpha |T_{N4}|\\T_{N4}表示以N4为根节点的子树,|T_{N4}|表示T_{N4}的叶结点数,这里等于2,但是为了得到通式,这里写为|T_{N4}| \tag{2}\]
剪枝后,它只剩下 N4 一个结点,光杆司令,这时候损失函数是:
\[C_\alpha(N4)=C(N4)+\alpha ,N4表示只有N4这个节点的树 \tag{3}\]
找“剪不剪枝都可以的\(\alpha\)” ,也就是找 \(C_\alpha(T_{N4})=C_\alpha(N4)\) 的 \(\alpha\) 。故有
\[C(T_{N4})+\alpha |T_{N4}|=C(N4)+\alpha \\得到:\alpha=\frac{C(N4)-C(T_{N4})}{|T_{N4}|-1} \tag{4}\]
可得,对于任意结点\(t\),记以 \(t\) 为根节点的子树为\(T_t\) ,只有 \(t\) 一个结点的树直接记为 \(t\) ,则得到计算结点 \(t\) “剪不剪枝都可以的\(\alpha\)” 的公式:
\[\alpha=\frac{C(t)-C(T_t)}{|T_t|-1} \tag{5}\]
问题得解:我们对每个內结点都用式 (5) 找出它”剪不剪枝都可以“ 的临界\(\alpha_0\),然后筛选出最小的 \(\alpha_0\) 对应的內结点剪枝。
三. CART 剪枝算法
输入:CART算法生成的决策树\(T^0\)
输出:最优决策树 \(T_\alpha\)
设 \(k=0\)
设\(\alpha_t = +\infin\)
对树,\(T^k\)各个内部节点 \(t\) 计算\(C(T_t)\) ,\(T_t\) 以及
\[\alpha(t) = \frac{C(t)-C(T_t)}{|T_t|-1}\\\alpha_t = min(\alpha,\alpha(t))\]
\(T_t\) 是以t结点为根节点的子树,\(t\)代表结点t,也表示只有 \(t\) 一个 结点的树,\(C(T_t)\) 是训练数据的预测误差(可以用基尼指数或者均方误差表征),\(|T_t|\) 是\(t\)为根节点的子树的叶结点数。
对\(\alpha(t)=\alpha\)的内部结点\(t\) 进行剪枝,对于剪枝后的结点\(t\) 采用多数表决法确认其类别,得到树 \(T^{k+1}\)
\(k=k+1\)
重复 3-5 ,直到\(T^k\)是一个三结点树(一个根节点两个叶结点)
对于得到的子树序列\({T_0,T_1,\cdots,T_n}\),采用交叉验证法选出最优子树\(T_\alpha\)