二分法是搜索算法中极其典型的方法,其要求输入序列有序并可随机访问。算法思想为
输入:有序数组nums,目的数值target
要求输出:如果target存在在数组中,则输出其index,否则输出-1
- 将原数组通过[left,right]两个索引划分范围,初值left=0,right=数组的最后一个元素
- 当left <= right时
- middle = (left + right)/2
- 判断nums[middle]是不是要查找的target,如果是则返回结果
- 判断nums[middle]> target,证明要查找的target在左边,因此right = middle – 1
- 判断nums[middle]< target,证明要查找的target在右边,因此left = middle + 1
- 没有查找到return -1。
形如下图:
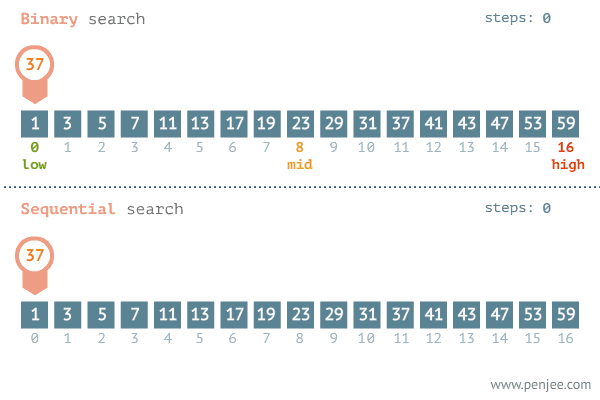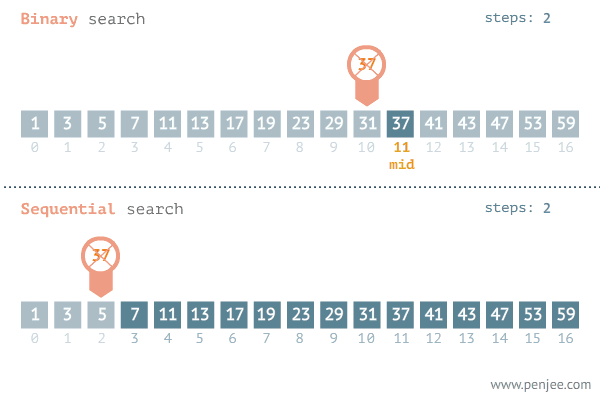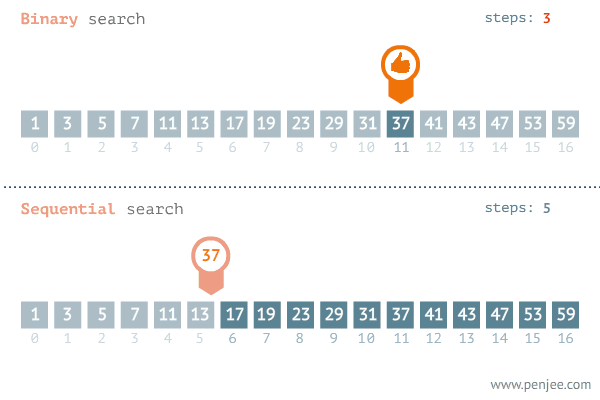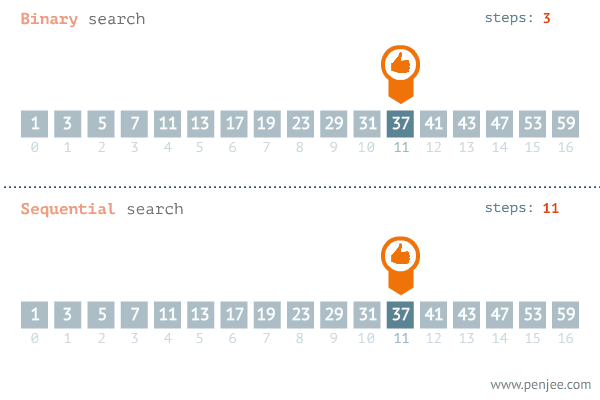
传统的二分法代码如下:
func binarySearch(nums []int, target int) int {left, right := 0, len(nums)-1for left target {right = middle - 1} else {left = middle + 1}}return -1}这里要注意两个问题:
- 上述算法中的第2步中
=的判断,即for left <= right还是for left < right。 - 上述算法2.2-2.4中的判断条件以及下一次查找区间的设置
- 返回值代表什么意思
for left<= right 中 = 的判断
首先对于第一个问题,=是否应该存在,取决于对于二分查找的初始化定义,例如:
- 如果二分查找遍历的区间采用
[left,right](数学中的双闭区间)的形式,考虑left==right即=成立的情况,则表示区间内只有单个操作数,这种情况还是需要处理,否则无法通过其余方式表示这种情况,所以此时=是必须的。 - 如果二分查找遍历的区间采用
[left,right)的形式,考虑left==right即=成立的情况,事实证明,这种情况并不应该存在,我们无法用[i,i)表示任何一个区间,所以,这种情况下,=就不是必须的。
判断条件以及下一次查找区间的设置
然后考察对于第二个问题,判断条件以及下一次查找区间应该如何设置?
注意:二分查找是一个经典的查找算法,其目的是查找到指定的位置或者值,并不仅限于查找到等于target的index这一种情况。
但无论怎样,二分查找本身有一个固定模式,即二分,就是从middle处将区间[left,right]分成两份,然后根据middle的情况查找(或者更新新的区间),因此,我们只需要考虑清楚如下三种条件时要怎么处理即可:
- 当遍历到nums[middle] == target时应该怎样处理(新的查找区间是什么),即当前值等于目标值
- 当遍历到nums[middle] > target时应该怎样处理(新的查找区间是什么),即当前值大于目标值
- 当遍历到nums[middle] < target时应该怎样处理(新的查找区间是什么),即当前值小于目标值
讨论完上述两个问题,其实二分法就有了一个固定的框架:
func binarySearch(nums []int, target int) int {left, right := 0, len(nums)-1for left target {// 当前值大于目标值时,如何处理(新的查找区间是什么)} else {// 当前值小于目标值时,如何处理(新的查找区间是什么)}} // 考虑返回值的意义return }返回值的含义
最后我们讨论返回值的含义这一话题。在传统的二分查找中,只有在两种情况下会返回:
- 查找到目标target,返回查找到的index
- 未查找到目标target,返回-1。(即文章最起始处 步骤3的含义)
这里返回值的含义表示target在nums中的index,该值只会出现在nums[middle]==target这一条件下。然而,刚才提到了二分查找不总是处理等式条件,因此我们总要思考两种返回值的含义:
- nums[middle]==target,这时return代表的是什么?
- 数组中不存在target,此时return的是什么,此时left、right代表什么?
这里我们举一个稍稍复杂一点的例子对二分查找进行分析。
- 搜索插入位置
- 在排序数组中查找元素的第一个和最后一个位置
搜索插入位置
题目要求如下:

这个问题要求返回两种返回值:
- 在数组中找到目标值,并返回其索引
- 如果目标值不存在于数组中,返回它将会被按顺序插入的位置
其中对于情况1,传统的二分查找算法就可以解决,而情况2,则需要借助于本部分要讲解的返回值的含义。
对于传统的二分法:
func binarySearch(nums []int, target int) int {left, right := 0, len(nums)-1for left target {right = middle - 1} else {left = middle + 1}}return -1}如果target能在nums数组中查找到,必定最终查找到一个[i,i]类型的区间,即区间中只有一个数字,否则区间就要再次进行二分。例如:如果要在下列数组中查找4所在的位置,查找过程如下,第三步时,查找区间为[2,3],有两个值,无法确定答案,则需要再次进行一次查找:
target == 4nums 1 2 3 4index 0 1 2 31 l r2 l r3 l r4 lr 那么最终我们处理的情况必定是对于区间[left,right]中,其中left == right,因此middle == left == right,此时nums[middle]和target的关系。
- nums[middle] > target,则需要从middle左侧继续寻找,right = middle – 1,注意此时left = middle,left > right
- nums[middle] right
所以此时,left指向的永远是大的那个值,right是小的那个值(因为left right,根据数组的有序性,nums[left] > nums[right])。
最后,我们考察该题,对于数组nums,如果目标值不在其中,那么其最终查找到的值只有两种情况:
- nums[middle] < target,此时nums[middle]应该是第一个小于target的值,如果要查找target所在位置,应该返回
大于middle的index,即left - nums[middle] > target,此时nums[middle]应该是第一个大于target的值,如果要查找target所在位置,应该返回
等于middle的index,用target替换middle位置的值,即left
因此,该题的结果,只需要修改传统二分查找的最后一行:
func binarySearch(nums []int, target int) int {left, right := 0, len(nums)-1for left target {right = middle - 1} else {left = middle + 1}}return left }在排序数组中查找元素的第一个和最后一个位置
题目要求如下:

注意这里查找的是元素第一次和最后一次出现的位置,这里我们以查找第一次出现的位置举例,后者同理。
考察我们在判断条件以及下一次查找区间的设置中强调的,考察二分查找的三种情况:
| 情况 | 分析 | 操作 |
|---|---|---|
| nums[middle] == target时,即当前值等于目标值 | 第一次出现的位置可能在当前值前面 | right = middle – 1 |
| nums[middle] > target时,即当前值大于目标值 | 第一次出现的位置在当前值前面 | right = middle – 1 |
| nums[middle] < target时,即当前值小于目标值 | 第一次出现的位置在当前值后面 | left = middle + 1 |
与之前不同的是当nums[middle] == target时,不再有返回值了,那么考虑最后返回值的含义,最终left > right时情况有如下3种:
| 情况 | 分析 | 操作 |
|---|---|---|
| nums[middle] == target | 此时,middle前的值必定<middle,而不是等于(只要等于,考虑上表的情况1,会使right = middle – 1) | return left |
| nums[middle] > target | 此情况不存在,因为如果有这种情况会继续使right=middle-1 | 不进行操作 |
| nums[middle] < target | 此时middle必定是target前的第一个元素 | return left |
经过上面的分析后,可以清晰的写出代码:
l, r := 0, len(nums)-1for l = target {r = m - 1} else {l = m + 1}} result := l而查找元素出现的最后一个位置,只需要反过来,最后return right即可。代码如下:
l, r: = 0, len(nums)-1for l <= r {m := (l + r) / 2if nums[m] <= target {l = m + 1} else {r = m - 1}} result := r总结
本文详细分析了二分查找的所有细节,对于二分查找处理的问题,我们常常需要更加关注本文讨论的后两个问题:
- 判断条件以及下一次查找区间的设置
- 返回值的含义
最后填充模版即可。
func binarySearch(nums []int, target int) int {left, right := 0, len(nums)-1for left target {// 当前值大于目标值时,如何处理(新的查找区间是什么)} else {// 当前值小于目标值时,如何处理(新的查找区间是什么)}} // 考虑返回值的意义return }