目录
写在前面
一、torch.optim.SGD 随机梯度下降
SGD代码
SGD算法解析
1.MBGD(Mini-batch Gradient Descent)小批量梯度下降法
2.Momentum动量
3.NAG(Nesterov acceleratedgradient)
SGD总结
二、torch.optim.ASGD随机平均梯度下降
三、torch.optim.Rprop
四、torch.optim.Adagrad 自适应梯度
Adagrad 代码
Adagrad 算法解析
AdaGrad总结
写在前面
优化器时深度学习中的重要组件,在深度学习中有举足轻重的地位。在实际开发中我们并不用亲手实现一个优化器,很多框架都帮我们实现好了,但如果不明白各个优化器的特点,就很难选择适合自己任务的优化器。接下来我会开一个系列,以Pytorch为例,介绍所有主流的优化器,如果都搞明白了,对优化器算法的掌握也就差不多了。
作为系列的第一篇文章,本文介绍Pytorch中的SGD、ASGD、Rprop、Adagrad,其中主要介绍SGD和Adagrad。因为这四个优化器出现的比较早,都存在一些硬伤,而作为现在主流优化器的基础又跳不过,所以作为开端吧。
我们定义一个通用的思路框架,方便在后面理解各算法之间的关系和改进。首先定义待优化参数,学习率为
,参数更新步骤如下:
1. 计算目标函数关于当前参数的梯度:
(2)
(4)
4. 根据下降梯度进行更新:
是一个batch的开始:
动量项通常设置为0.9或类似值。
参数更新公式如下,其中ρ 是动量衰减率,m是速率(即一阶动量):
(8)
(12)
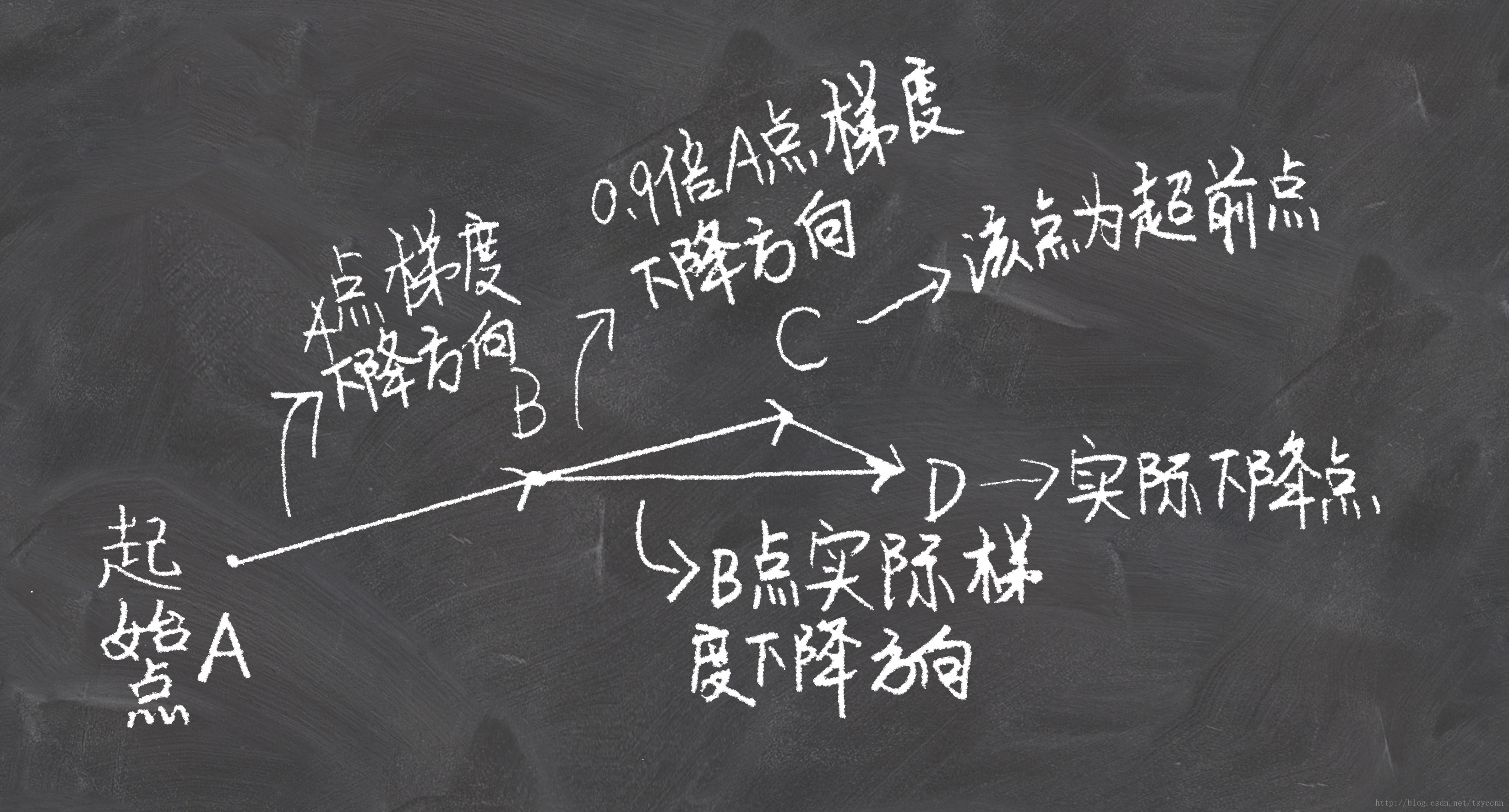
上式中的就是C点坐标(参数)。可以看到NAG除了式子(10)与式子(7)有所不同,其余公式和Momentum是一样的。
一般情况下NAG方法相比Momentum收敛速度快、波动也小。实际上NAG方法用到了二阶信息,所以才会有这么好的结果。
Nesterov动量梯度的计算在模型参数施加当前速度之后,因此可以理解为往标准动量中添加了一个校正因子。在凸批量梯度的情况下,Nesterov动量将额外误差收敛率从,然而,在随机梯度情况下,Nesterov动量对收敛率的作用却不是很大。
SGD总结
使用了Momentum或NAG的MBGD有如下特点:
优点:加快收敛速度,有一定摆脱局部最优的能力,一定程度上缓解了没有动量的时候的问题
缺点:a.仍然继承了一部分SGD的缺点
b.在随机梯度情况下,NAG对收敛率的作用不是很大
c.Momentum和NAG都是为了使梯度更新更灵活。但是人工设计的学习率总是有些生硬,下面介绍几种自适应学习率的方法。
推荐程度:带Momentum的torch.optim.SGD 可以一试。
二、torch.optim.ASGD随机平均梯度下降
ASGD 也称为 SAG,表示随机平均梯度下降(Averaged Stochastic Gradient Descent),简单地说 ASGD 就是用空间换时间的一种 SGD,因为很少使用,所以不详细介绍,详情可参看论文: http://riejohnson.com/rie/stograd_nips.pdf
'''params(iterable)- 参数组,优化器要优化的那些参数。lr(float)- 初始学习率,可按需随着训练过程不断调整学习率。lambd(float)- 衰减项,默认值 1e-4。alpha(float)- power for eta update ,默认值 0.75。t0(float)- point at which to start averaging,默认值 1e6。weight_decay(float)- 权值衰减系数,也就是 L2 正则项的系数。'''class torch.optim.ASGD(params, lr=0.01, lambd=0.0001, alpha=0.75, t0=1000000.0, weight_decay=0)推荐程度:不常见
三、torch.optim.Rprop
该类实现 Rprop 优化方法(弹性反向传播),适用于 full-batch,不适用于 mini-batch,因而在 mini-batch 大行其道的时代里,很少见到。
'''params - 参数组,优化器要优化的那些参数。lr - 学习率etas (Tuple[float, float])- 乘法增减因子step_sizes (Tuple[float, float]) - 允许的最小和最大步长'''class torch.optim.Rprop(params, lr=0.01, etas=(0.5, 1.2), step_sizes=(1e-06, 50))优点:它可以自动调节学习率,不需要人为调节
缺点:仍依赖于人工设置一个全局学习率,随着迭代次数增多,学习率会越来越小,最终会趋近于0
推荐程度:不推荐
四、torch.optim.Adagrad 自适应梯度
该类可实现 Adagrad 优化方法(Adaptive Gradient),Adagrad 是一种自适应优化方法,是自适应的为各个参数分配不同的学习率。这个学习率的变化,会受到梯度的大小和迭代次数的影响。梯度越大,学习率越小;梯度越小,学习率越大。
Adagrad 代码
'''params (iterable) – 待优化参数的iterable或者是定义了参数组的dictlr (float, 可选) – 学习率(默认: 1e-2)lr_decay (float, 可选) – 学习率衰减(默认: 0)weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)initial_accumulator_value - 累加器的起始值,必须为正。'''class torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0)Adagrad 算法解析
AdaGrad对学习率进行了一个约束,对于经常更新的参数,我们已经积累了大量关于它的知识,不希望被单个样本影响太大,希望学习速率慢一些;对于偶尔更新的参数,我们了解的信息太少,希望能从每个偶然出现的样本身上多学一些,即学习速率大一些。这样大大提高梯度下降的鲁棒性。而该方法中开始使用二阶动量,才意味着“自适应学习率”优化算法时代的到来。
在SGD中,我们每次迭代对所有参数进行更新,因为每个参数使用相同的学习率。而AdaGrad在每个时间步长对每个参数使用不同的学习率。AdaGrad消除了手动调整学习率的需要。AdaGrad在迭代过程中不断调整学习率,并让目标函数中的每个参数都分别拥有自己的学习率。大多数实现使用学习率默认值为0.01,开始设置一个较大的学习率。
AdaGrad引入了二阶动量。二阶动量是迄今为止所有梯度值的平方和,即,从这里我们就会发现
(13)
(14)
AdaGrad总结
AdaGrad在每个时间步长对每个参数使用不同的学习率。并且引入了二阶动量,二阶动量是迄今为止所有梯度值的平方和。
优点:AdaGrad消除了手动调整学习率的需要。AdaGrad在迭代过程中不断调整学习率,并让目标函数中的每个参数都分别拥有自己的学习率。
缺点:a.仍需要手工设置一个全局学习率, 如果设置过大的话,会使regularizer过于敏感,对梯度的调节太大
b.在分母中累积平方梯度,由于每个添加项都是正数,因此在训练过程中累积和不断增长。这导致学习率不断变小并最终变得无限小,此时算法不再能够获得额外的知识即导致模型不会再次学习。
推荐程度:不推荐
接下来adam相关的将是重点,敬请期待。。。