我将用一整天突击，崭新的一本书，从0到期末80+，（仅针对本校逆天考点进行总结）
完本总结：总计历经两天半，共计15小时，总计30+页，仅带来个人的复习思路与心路历程
写本博客原因？
- 马上期末考试，整本书从来没有看过，尝试0基础一天学完，突破自己。
- 网上没有完全符合本课程的详细汇总(其中一篇总结不错，后面会提)，尤其网课质量极差，是极差！
- 针对特定细小问题没有明确解答，自己深受其害，自己受过的苦，争取能帮到别人（虽然没人看）
- 因为热爱
第一章 引言
既然是引言，大体了解就行，主要考在网安的一些基本简单问题，如攻击类型，基本目标，密码体制分类，保密系统模型，及简单古典密码
1.攻击类型
被动攻击：即窃听，针对保密性， 是难以检测的，重点在预防
主动攻击：中断，篡改，伪造 检测恢复
2.密码技术是保障数据安全的关键技术。
信息在社会中的地位和作用越来越重要，则其安全愈发重要，而密码学是保障信息安全的核心技术。可以说没有密码学就没有信息安全。
3.保密通信系统
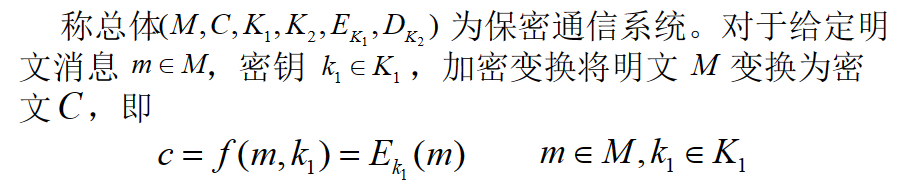
即图1-5
保密系统满足下面要求：
- 系统即使达不到理论上是不可破的，即 ，也应当为实际上不可破的。就是说，从截获的密文或某些已知明文密文对，要决定密钥或任意明文在计算上是不可行的。
- 系统的保密性不依赖于对加密体制或算法的保密，而依赖于密钥。这是著名的 Kerckhoff 原则。
- 加密和解密算法适用于密钥空间中的所有元素。
- 系统便于实现和使用。
4.密码体制分类
密码体制从原理上分为单钥体制（流密码，分组密码）和双钥体制两大类
唯密文是最难攻击的，因为他知道的最少
5.古典密码
最古老的三个非常简单，有数学基础给出式子就能做，着重说一下多表代换密码。没有技巧，全是计算总之，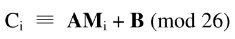
用这个公式反复变换，是可以解决多表问题的
首先会给出n,N,一般n也就是2或3，多了太难算了，N就是26，给出一串字母和一个密码矩阵A
n是几，给的字母串就拆成几个一组a[i]，如果是明文，则密文C = A * a[i],连起来就对了，如果给的是密文，恭喜你，中间需要求逆矩阵，作为网安的倒霉蛋
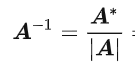就老实用这个算求吧，我觉得是真麻烦M = A~ * a[i]，反正可以求
这个例题我试了，可以的，学加写这一章用了一个小时，要加速了呀
第二章 流密码
高深的知识，如果有兴趣可以讨论，目前只针对考试，完全不需要学m序列等等的耗时间的东西。首先知道流密码是啥，再者密钥流生成器，寄存器，练习题，🆗了就
1.什么是流密码
课本给的是
说人话，就是密钥发生器通过密钥k产生了密钥流，其中对逐比特进行加密，所以他是流
2.移位寄存器是流密码产生密钥流的一个重要组成部分，没什么好说，看题吧
例题2.2
这种题初看很吓人，仔细看你会发现，就是按照这个流程图，跟着他箭头走，循环就完了，
例题2.3
这个c其实就是开关，把控对此是否进行异或而已
习题2.1 2.3
其实这就是一类题，流密码再考别的就超了讲真
第三章 分组密码
搞清楚，什么是分组密码，他与流密码都是单钥体制，区别在分组密码无记忆性且数量不同，再者怎么操作的，运行模式几种，怎么用，画图呢，什么是feistel结构，结构设计，des的基本操作，多重的des
1.什么是分组密码
将明文划分为长为n的组x(x0,x1,…,xn-1)，各组在密钥k=(k0,k1,…kt-1)控制下变换成等长的数字序列y=(y0,y1,…ym-1)。
他实际上就是对字长为n的数字序列的代换密码而已（一般m=n）
分组方式，当然让他m=n最好，要是不够就补零,其实并没有要求明文的加密长度和密文加密长度一样的
2.扩散和混淆是Shannon提出的设计密码系统的两个基本方法(分组密码安全设计性原则)
扩散：使明文与密文之间的统计关系变得尽可能复杂，以使敌手无法得到密钥。明文每一比特变换尽量多的影响密文序列的变化，以隐蔽明文的统计特性（雪崩效应）
混淆：使密文与密钥之间的统计关系变得尽可能复杂，以使敌手无法得到密钥
P盒(置换)用于扩散
S盒(代换)用于混淆
3.Feistel结构
按课本上的话说，很多分组密码结构本质都基于Feistel结构。
Feistel提出利用乘积密码可以获得简单的代换密码，乘积密码指顺序地执行两个或多个基本密码系统，使得最后结果的密码强度高于每个基本密码系统产生的结果Feistel 还提出了实现代换和置换的方法。其思想实际上是 Shannon 提出的利用乘积密码实现混淆和扩散思想的具体应用。
将每组明文分为左右两半L0和R0，n轮迭代后再合在一起产生密文分组
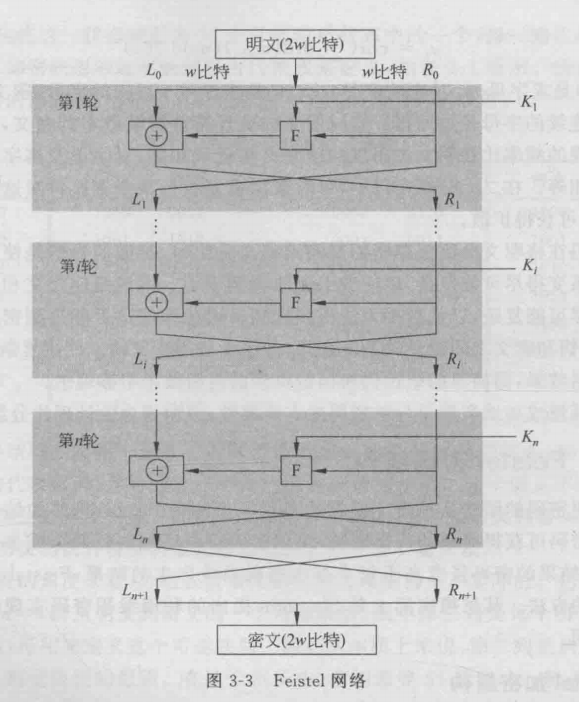
图挺关键的，
第i轮迭代（代换）： Li=Ri-1(左等右上) Ri=Li-1⊕F(Ri-1,Ki) （右等左上异或F即右上和K）
最后一轮交换左右两半数据（置换）
解密和加密本质过程一样，密文作为输入，但使用子密钥Ki的次序和加密相反（这一特性保证了加密和解密可用同一算法）
总之，用自己的话说，这个密码就是：分成左右两边，右边用F进行加密，和左边异或一下，和这一轮原始的进行交换，进行n轮迭代，最后置换一下，再合在一起，听到这里怎么这么熟悉，怎么和des这么像，巧了，des就是这种结构。
4.des加密
众所周知，des16轮轮密钥，按64比特进行分组
1首先初始置换，将第58个比特放在第一个位置上，逆初始置换也一样，第四十比特放在第一个位置上
2轮结构
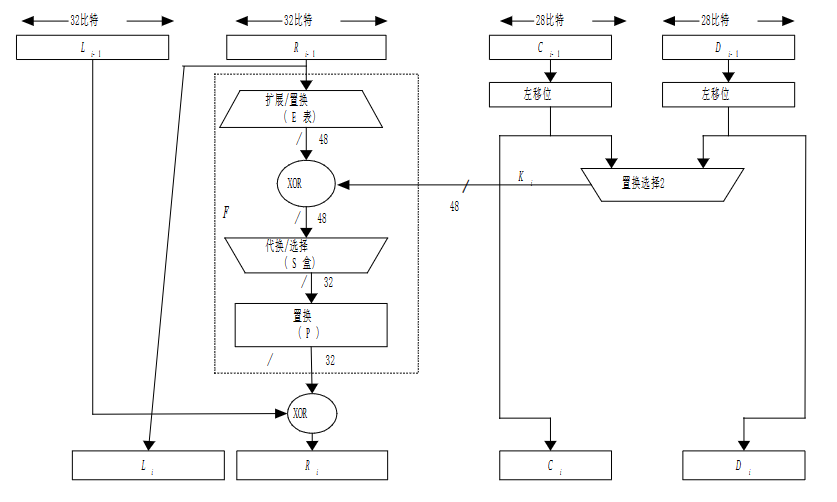
将右边的32 扩展到48 与48的密钥进行轮密钥加，得到48的结果再S盒压缩到32，通过置换得到32的轮函数输出，再与左边进行一次异或，得到本次的R结果。一轮就结束了
如果有条件，我很想讲讲，现就粗略地说一下大概
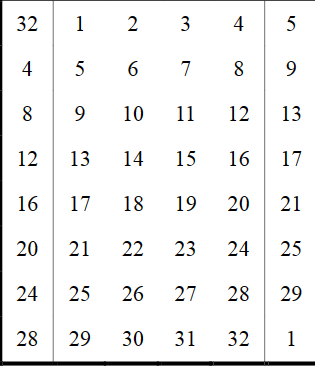
扩展运算就是把四个，边上的前一个和后一个扩展了
轮密钥加就是8组6比特变成4比特，具体操作就是把6比特输入看成一个二进制数，16位选行，2-4选列，查S盒书成即可
3密钥产生
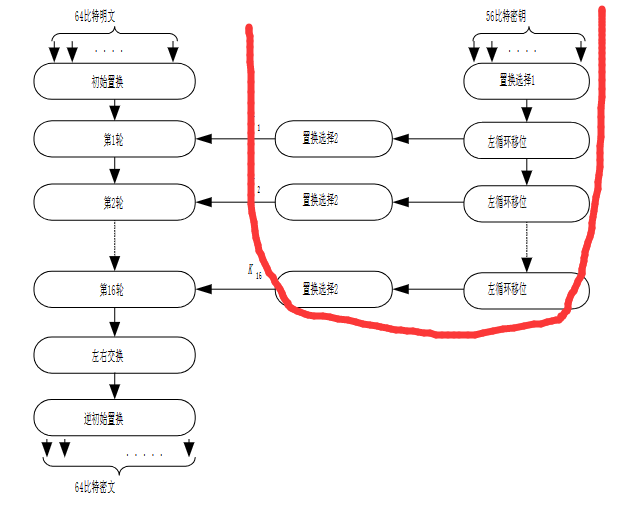
大概就是先选择1，压缩到56比特密钥，分成两份再置换，再i轮循环左移，通过置换选择2得到48位密钥
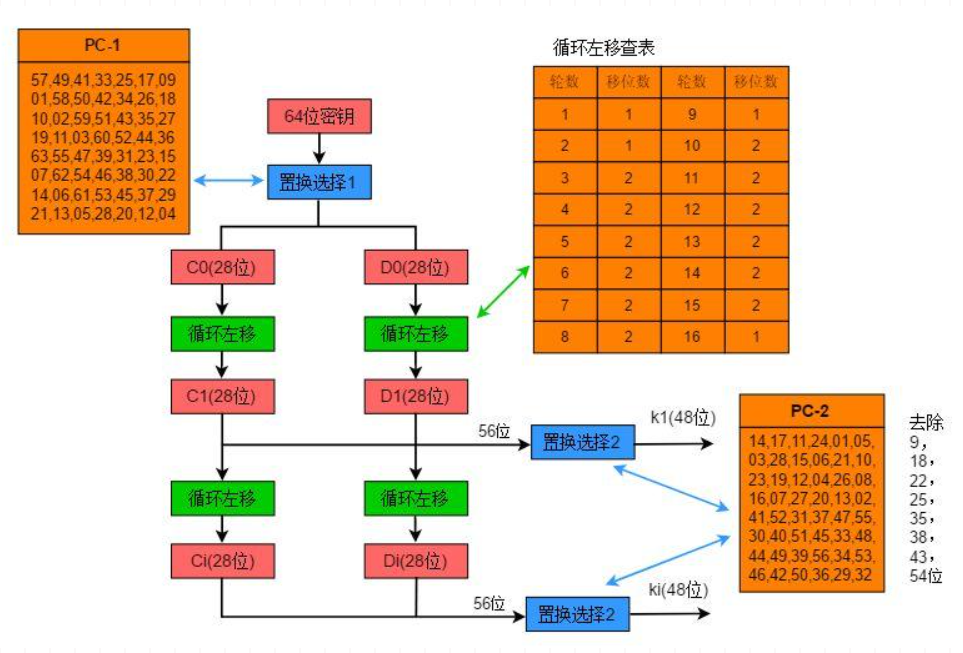
4解密，同意算法，相反顺序
5.下一步，二重des
就是使用两个加密密钥K1、K2密钥长度112，强度极大增加，但是如果一个K3可以正好替代这俩，
那么恭喜你之前两个密钥白找了
下面话锋一转，我也没看懂，得出结论，二重不好考，也考不到，嗯对
接着便是两个密钥的三重，三个密钥的三重，迭代吗，如果找的巧了总会降重的，但是，几率很小，安全性也极大增强了
6.分组密码的运行模式
ECB(电话本)模式 各明文组以同一密钥加密
CBC(密码分组链接)模式 加密的输入是当前明文组和前一密文组的异或
CFB(密码反馈)模式 每次处理j位输入，上次密文加密产生伪随机再与当前明文异或
OFB(输出反馈)模式 与CFB不同的是加密的输入是前一次加密的输出(与明文异或的那个)
经过我的多方考察，这个竟然是必考的，当然写这个博客也是来自这师哥的总结，写的真心不错，很清晰，在一众劣质视频（也不是，就是没什么用）下的一股清流。
链接(25条消息) 现代密码学期末总结_现代密码学第四版答案 杨波_夏日 の blog的博客-CSDN博客
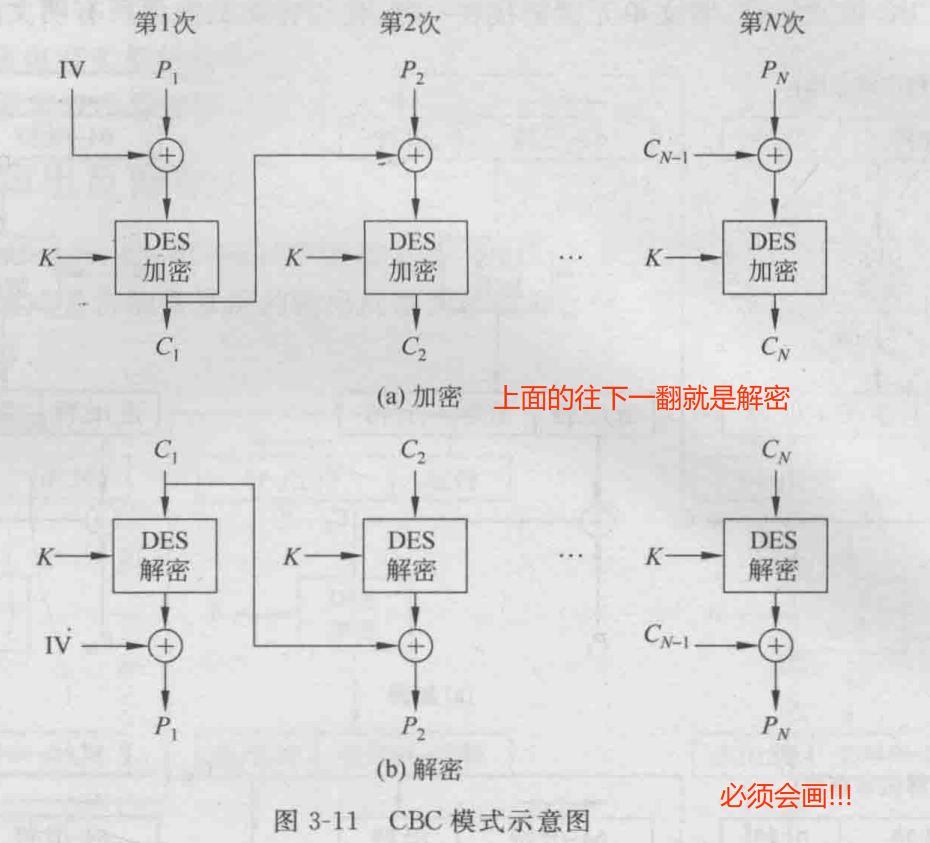
加密: Ci= Ek[Pi⊕Ci-1] (可认为C0=IV) 解密:Pi= DK[Ci]⊕Ci-1
工作模式为：它一次对一个明文分组加密，每次加密使用同一密钥，加密算法的输入是当前明文分组和前一次密文分组的异或，因此加密算法的输入不会显示出这次的明文分组之间的固定关系，所以重复的明文分组不会在密文中暴露出这种重复关系 。
7.AES
大boss，众所周知，AES替代DES，成了最流行的加密算法，（这一章真长，看的我泪流满面）
好了，首先有一点GF(2^8)就是在这个域里面的多项式运算，(mod x8+x4+x3+x+1)是其中的不可约多项式
所以这个就衍生出了一类题目：字节代换
这种类型的，首先第一步要求逆元了，没错，拓展欧几里得算法，我真服了是，我真是破防了，就这么一个简单的多项式除法，我浪费了一个小时竟然没有找到任何一个可以讲清楚的，好，破防了。说回正事
第二步，左边仿射矩阵是固定的，加上的矩阵也是固定的，逆元要从下往上写，计算就好了，真是，这么小的问题浪费我这么多时间。
AES简单看一下吧，就包括下面几个功能，不想剖析了，
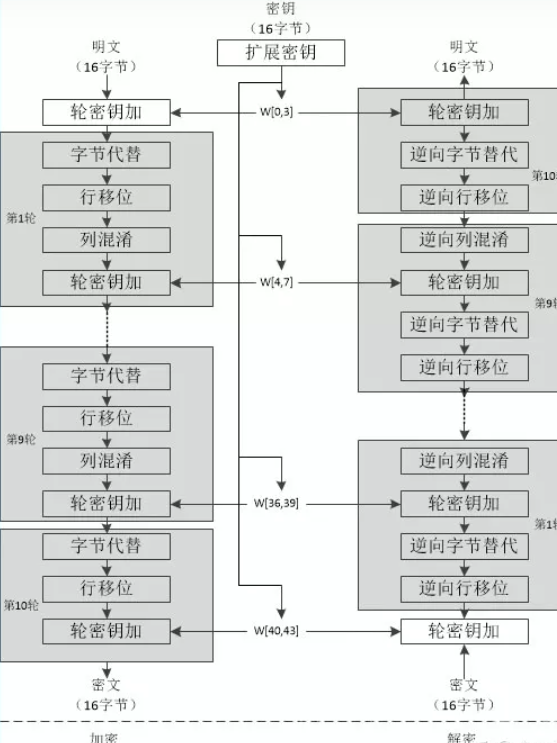
AES轮函数包括字节代换、行移位、列混合、密钥加
1️⃣ 字节代换：根据S盒把明文块的每一个字节都替代成另外一个字节
2️⃣ 行移位：如第1行不变，第2行循环左移C1个字节，第3行左移C2个字节，第4行移C3 要根据表
3️⃣ 列混合：输入数组每一列和修补矩阵的二维常量数组做矩阵相乘，得到对应的输出列。
4️⃣ 密钥加：输入数组的每个字节a[i,j]与密钥对应位置的字节k[i,j]异或一次，就生成了输出值b[i,j]
盲猜这个不会考，大致了解流程就可
8.SM4，大概不考
我国公用的第一个商用密码
加密：Xi+4=F(Xi,Xi+1,Xi+2,Xi+3,rki)=Xi⊕T(Xi+1⊕Xi+2⊕Xi+3⊕rki)（i=0,1,2…31）
后经反序R处理：(Y0,Y1,Y2,Y3)=(X35,X34,X33,X32)=R(X32,X33,X34,X35)
解密算法和加密算法相同，轮密钥使用顺序相反
(25条消息) SM4国密算法整理-流程图_sm4流程图_Berte_Yu的博客-CSDN博客讲的很详细了，可以了解
本章习题，如果有证明题，考到算你倒霉
习题3.2
据说要考这个，我真没什么好说的，浅浅记一下吧
经典习题3.3
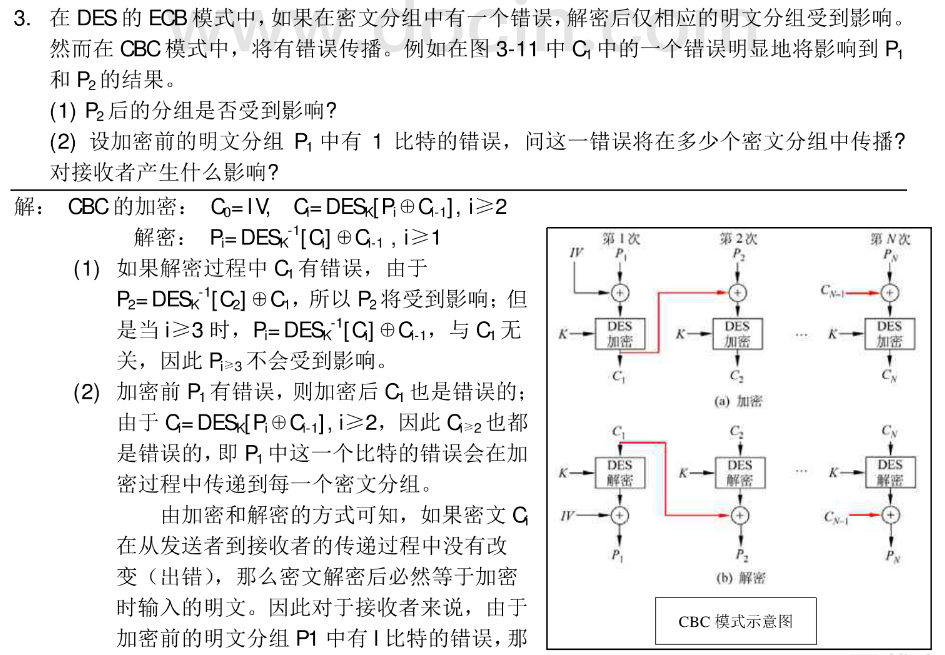
总结一下就是CBC的加解密，C1影响P1的结果，肯定是解密途中，那么解密时下一组的P其实只与当前的C和上一组的C 有关，而C1是无法决定后面的，所以不影响后面分组
而加密时，P1的错误会无限贯彻到其下一个之中，所以会全错，而对他解密时，其实是一个逆向的过程，逆回来其实和最初是一样的P1，即使P1错一点，但是明文是没错的。破案了哦
第四章 公钥密码
主要考点，群环域，欧几里得，公钥密码体制的基本概念，框架，满足要求，加上RSA的经典三连，背包体制，椭圆曲线不考吧。总体看起来和网安数学基础有很大关系，实则我想多了。
那么通过课后习题来看主要考点
1.群环域，拥有乘法逆元基本就是域了，不用多说了
2.欧几里得，欧拉定理，中国剩余定理等等，太熟悉了
3.公钥密码体制
首先他抛开了原始的代换置换，变成了由数学函数进行，是质变，而且是非对称，俩密钥，不得不说，是现代密码学史一大革命，为了解决密钥分配与数字签名提出。
说句题外话，我觉得他解决密钥分配的问题，就是让密钥不再运输了，每个人都有自己的密钥，不就不用配送了吗
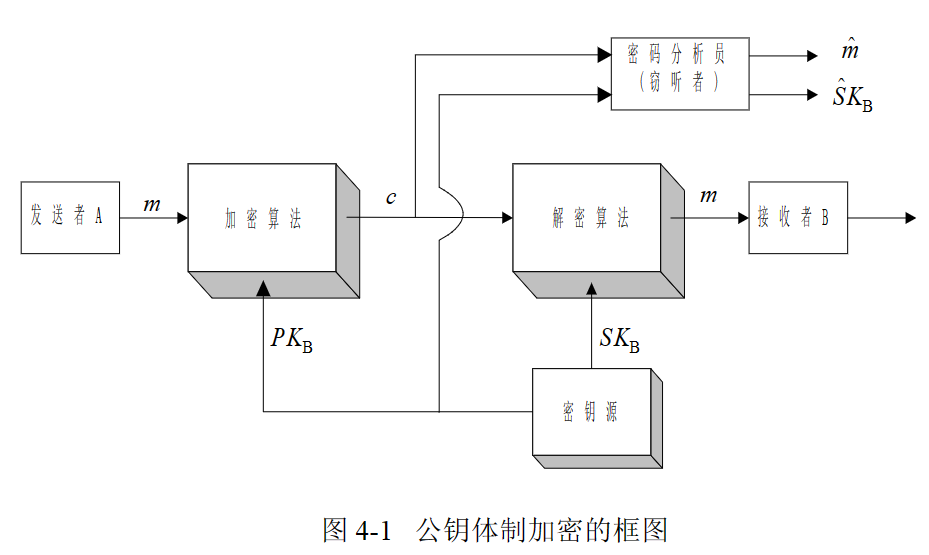
解释一下：第一个图，首先接收消息的端系统 产生一对密钥，一个公开，一个自己留着，如果A想给B发一个消息m，那他得通过公开的PK加密，B收到后，用自己的SK解密，这个SK只有他自己知道，所以窃听的人也没法解密，这也就是公钥密码体制的原理
那么如果是A的端系统生成的密钥，公开一个PK给B 会怎么样呢，根据原理，此时A是用他私钥进行加密的，所以里面内容除了他自己，谁也无法篡改，别人都可以通过PK破译他说什么，但是无法否认，这只能是A发出的，说明来源可靠。
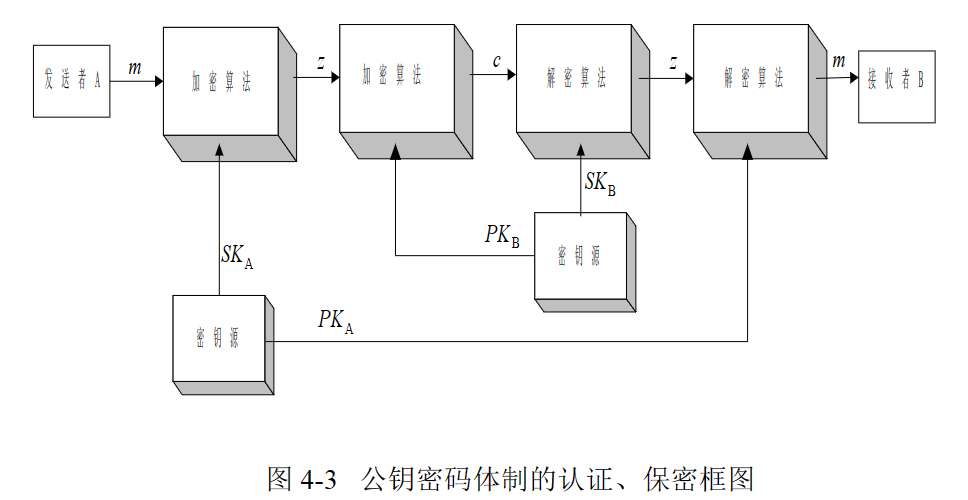
那么两个结合一下，B先通过PKA证明这个是A发的，没错，再通过自己私钥对m解密，得到里面内容，双重保险，好啊，是不是很熟悉，因为很靠近数字签名了。
而公钥体制需要满足的要求，通过上面描述大概也都清晰了，最后再说一点，他最核心的要求在于找到一个合适的单陷门函数，什么是单陷门函数，就是~
若y=f(x)，已知x很容易计算y，但已知y很难计算x（单向性）。特别的是存在一个z使得知道了z那么就很容易由y计算出x，那么z则称为陷门，也就是后门。
4.经典RSA 无需多言
证明与安全性，肯定没问题，不会考反正，那么怎么计算相关题目呢
例题 1 RSA加密体制中，接收方的公开钥是(e,n)=(5,35)，接收到的密文是C=10，求明文M
例题 2 假设明文m=5，e=7，p=11，q=13，给出RSA的加密解密过程
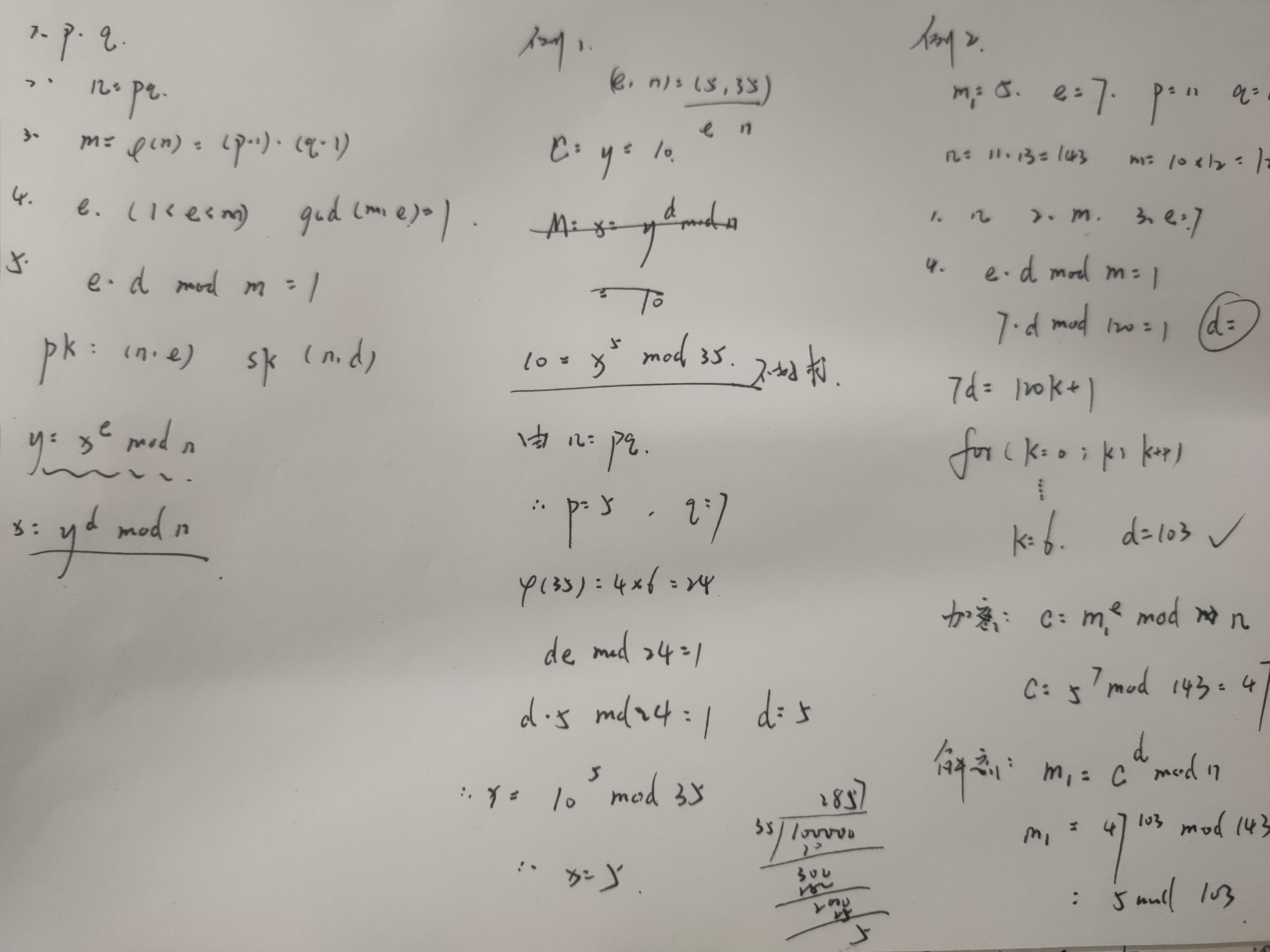
5.背包体制
他都叫背包了，什么成分懂得都懂，言归正传，假如A想发送一条信息，A首先要具有私钥，并且该密钥是通过背包问题传递的，该私钥可以生产一个公钥，发送消息之前必须先使用公钥进行加密，消息的合法接收者使用私钥等已知信息进行解密，这就是背包加密算法的总体思路。
(25条消息) 背包密码体制原理大白话讲解及Python实现_Always–Learning的博客-CSDN博客博主讲的特别清晰
假如有一个背包，背包的重量已知，将这个背包的重量与我们已知的超递增序列中的最大值进行比较，如果背包的重量小于这个数，那么这个数不在背包中，如果重量大于或等于这个数，那么这个数在背包中，用背包的重量减去这个数，得出的结果继续与序列中的下一个数进行比较，重复比较直到比较完为止。如果背包的总重量减到0则该背包问题得出解，反之则无解。
这篇博客讲的太清晰了，醍醐灌顶，就不再复制了，虽然这个可能并不会考。
下面进行本章习题12345 13
没有技巧，全是感情，还有就是我就很不明白，为什么要考一个13题Elgamal算法的
老规矩，什么是elgamal？
ElGamal加密算法可以定义在任何循环群G<span data-mathml="G”>上。它的安全性取决于G<span data-mathml="G”>上的离散对数难题。加密算法由三部分组成：密钥生成、加密和解密。
我大概明白为什么考他了，原来他就是经典公钥体制，是本章最初流程图的实际应用，加上和rsa的合体嘛
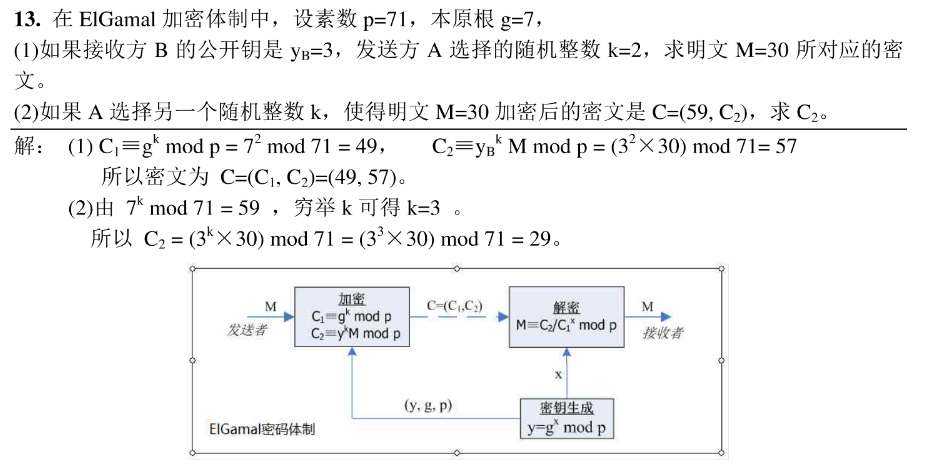
对照rsa中，素数p 就是 n (n = pq) 公钥yb，随机整数 k 就是 e ,则 我发现还是不能对照，老实记下来吧还是C1 = g^k mod p C2 = yb^k * M mod p,记住两个公式就结束了。
第五章 密钥分配与密钥管理
走到这里，一共耗费了9个小时，好久没学习这么认真了，已经结束2/3了，剩下的567考的较少，往后更少，继续，再接再厉。
言归正传，第五章主要考对称公钥体制的管理、分配、证书、密钥交换，及几个小例子
1.密钥分配
就对称加密来说，通信双方必须使用相同的密钥并且该密钥要对其他人保密，为了减少攻击者攻陷密钥所危害的数据量，要频繁更换密钥。因此，任何密码系统的强度取决于密钥分发技术。对A和B来说，密钥分发的方式有：
A选择一个密钥后以物理的方式传递给B
第三方选择密钥后物理地传递给A和B
如果A和B先前或者最近使用过一个密钥，则一方可以将新密钥用旧密钥加密后发送给另一方
如果A和B到第三方C有加密连接，则C可以在加密连接上传送密钥给A和B
在方式1和2中，人工交付密钥，在分布式系统中是不实用的。在分布式系统中，任何给定的主机或者终端都可能需要同时与很多其他主机以及终端交换数据，因此每个设备都需要动态提供大量的密钥。如果是端到端加密的网络，或者IP层执行，那么网络中每对想要同学的主机都要一个密钥，若有N台主机，那么密钥的数量就是N(N-1)/2个。
方式3中，可以用于链接加密和端到端加密。但是如果攻击者成功获得下一个密钥，随后的密钥都会泄露，潜在的数百万密钥都必须进行重新分发
方案4中，负责为用户分发密钥的密钥分发中心是必需的，且为了密钥的分发，每个用户都需要和密钥分发中心共享唯一的密钥。
2.公钥加密体制的密钥管理
简单密钥分配和具有保密性的分配，书上内容讲的很好，有点累了，看的头大，又多又难说，如果回头有时间我补上再。直接下一步，Diffie – Hellman密钥交换，是利用离散对数进行的
这个也忘了：设m是正整数，a是整数，若a模m的阶等于φ (m)，则称a为模m的一个原根不重要也不会问
Diffie – Hellman密钥交换大概翻译一下就是，一人生成一个随机数，自己藏着，都对a^X mod q处理一下发给对方，然后分别用自己的数计算出来的次方结果是一样的，相当于共同的秘密密钥，而敌手只能攻破离散对数运算才能破解，是不可能的。
做个例题
在Diffie- Hellman密钥交换过程中，设大素数p=11,a=2是p的本原根。 是不是特别简单
(1) 用户A的公开钥YA=9,求其秘密钥XA。
(2)设用户B的公开钥YB=3,求A和B的共享密钥K
1️⃣ YA=aXAmod p = aXAmod p 即 9=2XAmod 11 所以 XA=6 (考试时一个一个试就行)
2️⃣ K=YBXAmod p = 36mod 11 =3
3.重中之重，密钥分割
门限秘密分割
秘密 s 被分成 n 份毫无相关的部分信息，每一部分信息称为一个子密钥，由一个参与者持有，只有至少拥有 k 份子密钥时才能恢复出秘密 s，这种方案为 (k,n) –秘密分割门限方案，k称为方案的门限值 。Shamir门限方案就是一种门限秘密分割方案，他是基于拉格朗日插值公式的
确实是这样的，记住公式，计算还是比较简单的。
第六章 消息认证与哈希函数
主要考MAC是什么，使用方式，哈希函数，满足哪些条件，md5描述、细节和一些基本使用方式
1.消息认证码（MAC）
消息认证码是指消息被一个密钥控制的公开函数作用后产生的、用作认证符的、固定长度的数值，也称为密码校验和
将通信双方共享的密钥K和消息m作为输入，生成一个关于K和m的函数值MAC，将其作为认证标记(Tag)。发送时，将消息和认证码同时发送给接收方，若接收方用消息和共享密钥生成相同的消息认证码，则认证通过。
消息认证码用于保证数据的完整性。即防止数据被非授权用户篡改。需要注意的是：仅加密是无法保证数据的完整性的（如对ECB模式的攻击），因此需要认证。常见的消息认证码包括以下几类：
- 基于分组密码的MAC
- 基于带密钥的Hash函数的MAC
- 基于泛Hash函数的MAC
2.哈希函数
哈希函数 H 是一公开函数，用于将任意长的消息 M 映射为较短的、固定长度的一个值 H(M) ，作为认证符，称函数值 H(M) 为哈希值或哈希码或消息摘要。
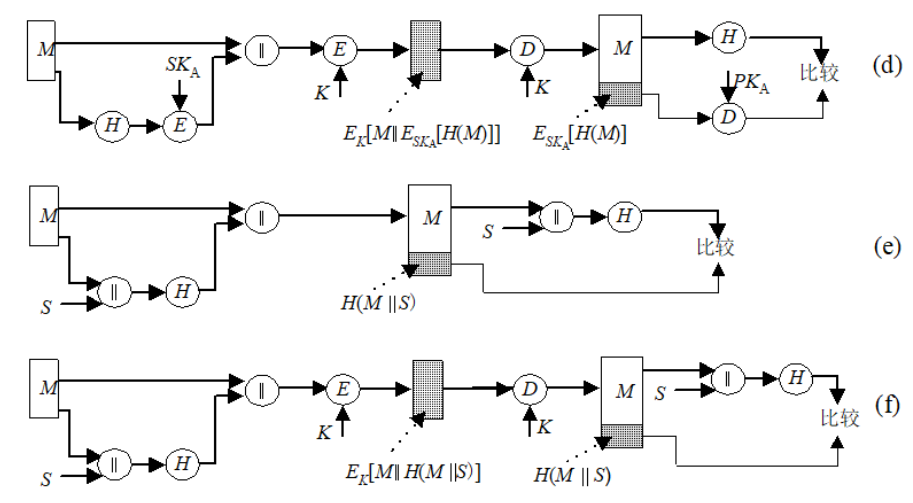
上述六种基本使用方式
1.链接后用单钥加密 2.仅对哈希码加密 3.用公钥和发送方秘密钥仅加密哈希码 4. 同3先加密后再与消息链接，链接后采用单钥加密算法
5.两者共享一个秘密值S和M链接起来哈希值 6. 同5链接后增加单钥加密 多看两遍自然就明白了，通俗易懂
哈希函数满足的条件：
1.输入任意长，2.输出固定长度 3.已知 x 求 H(x) 容易 4 . 已知 h 求 H(x) = h 不可行，因为单向性，说起这个来
已知x，找出y (y≠x) 使得H(y)=H(x)在计算上是不可行的，若单向函数满足这种性质则称其为弱单向哈希函数
找出任意两个不同的输入x、y，使得H(x)=H(y)在计算上是不可行的，若单向函数满足这种性质则称其为强单向哈希函数
已知一个另找一个使得H函数相等是弱单向，任意给倆使其H函数相等是强单向
如果哈希函数对不同的输入可产生相同的输出，则称该函数具有碰撞性。
抗弱碰撞哈希函数：对于任意给定的x，找到满组足y≠x且H(x)=H(y)的y在计算上是不可行的
抗强碰撞哈希函数：找到任何满足H(x)=H(y)的x,y在计算上是不可行的
3.MD5
了解一下就够了，不再赘述了
MD5的作用是让大容量信息在用数字签名软件签署私人密钥前被”压缩”成一种保密的格式（就是把一个任意长度的字节串变换成一定长的16进制数字串）
MD5算法具有以下特点：
1、压缩性：任意长度的数据，算出的MD5值长度都是固定的。
2、容易计算：从原数据计算出MD5值很容易。
3、抗修改性：对原数据进行任何改动，哪怕只修改1个字节，所得到的MD5值都有很大区别。
4、强抗碰撞：已知原数据和其MD5值，想找到一个具有相同MD5值的数据（即伪造数据）是非常困难的。
如上就够了。
第七章 数字签名和认证协议
题目起的已经很清晰了，本章就干两件事情，1 数字签名，2 认证协议
1.数字签名
正如前文提过经典公钥密码体制其实就是数字签名
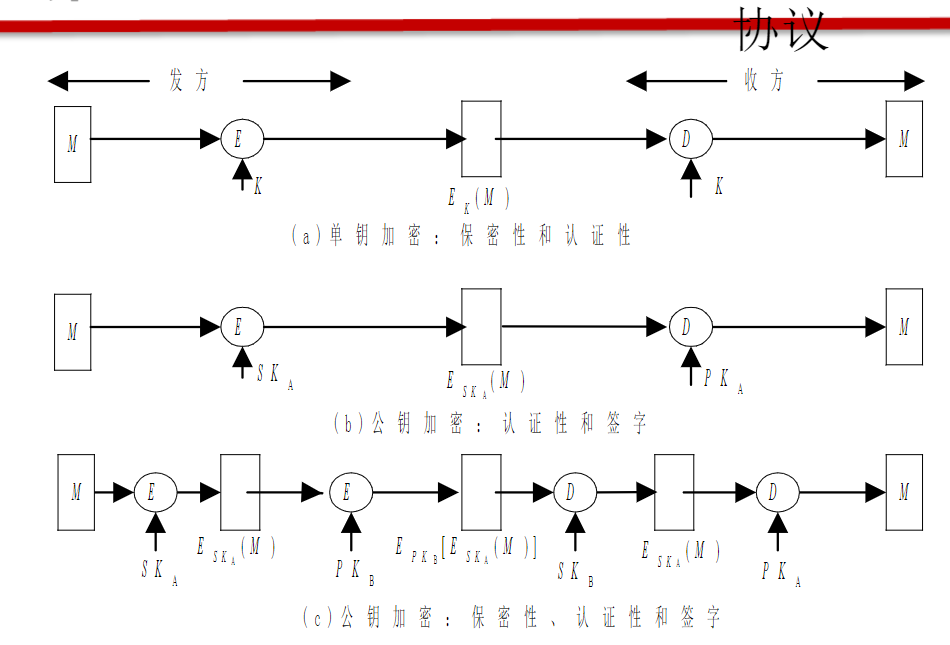
即1给2发消息，1先通过自己的私钥加密和密文一起通过2的公钥加密，2再通过自己的私钥解密和1的公钥解密签名，确保是1发的
所以我们可知，其实数字签名的功能也就在于1认证，2防抵赖，3保证完整性
2.对于数字签名标准（DSS）
DSS与RSA不同，只能用于提供数字签名而无法单独加密，RSA的过程如流程图显而易见，用自己的公钥加密哈希值和消息一起发给2，2用1的公钥解密签名再用自己的私钥解密消息，求哈希，如果哈希一样就说明没问题。而DSS实则是双签名，流程类似，只是多了随机数k再者加密过程先用自己的私钥和一个全局公钥加密，最后srm三方验证，其实我一直不理解k是怎么传递的，我个人认为是和消息一起传递的，只是图中没显示。
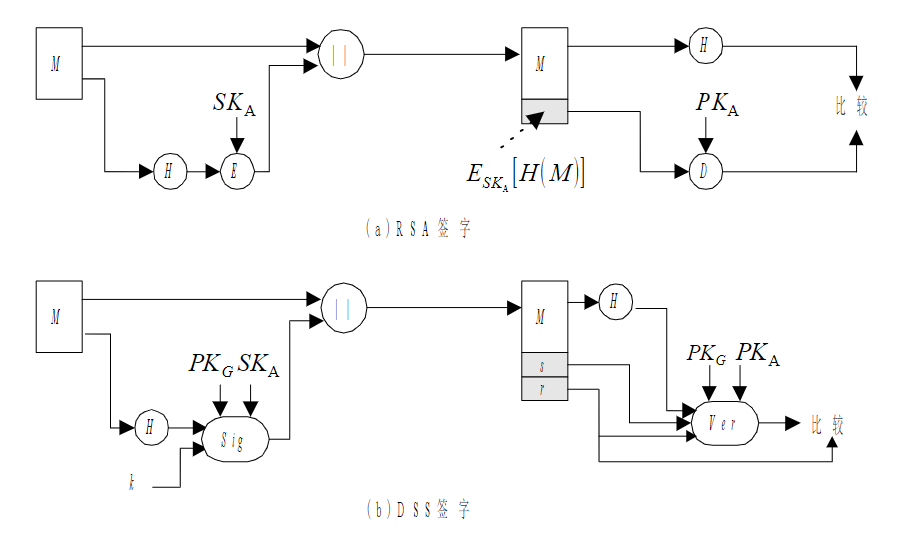
3.数字签名算法DSA
他就是基于ElGamal 和 Schnorr两个签名方案设计的，也是基于离散对数的安全性
我大概明白之前的k是怎么回事了，就是放在消息进行传递
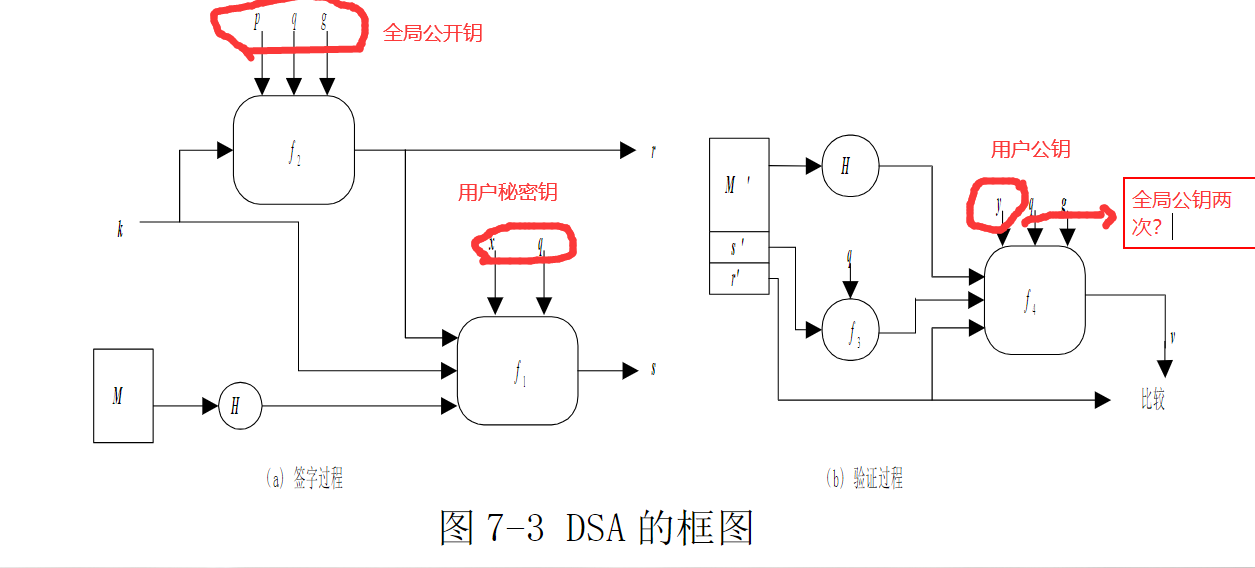
讲真我觉得有点乱，为什么全局公钥可以两次解密，要是全局私钥的话，岂不是人尽皆知，不过依照教程确实是公钥，一切流程也说得通了，以后再做研究。
4.认证协议
1.相互认证
首先两个用户在建立密钥时要考虑保密性和实时性，保证实时性可以通信戳和询问-应答，不必多说，最重要的：
认证协议是什么？——实体认证，身份认证， 数据源认证，消息认证。用来防止篡改，假冒，否认等攻击。
认证，即为鉴别，是通信过程中其他所有安全措施实施的基础
– 认证至少涉及到两个独立的通信实体
– 认证过程=认证协议，包含三个方面的含义
- 身份认证：主要验证消息发送者所声称身份的真实性
- 数据源认证（消息认证）：主要验证消息中某个生成属性的真实性
- 密钥建立认证：致力于产生一条安全信道，用于后继的安全通信会话
当认证主体接收到一个消息时，
- 他需要识别出消息在传递过程中是否被修改过；
- 其次，需要判断消息发送的时间以方便判断消息是否仍然有意义；
- 最后，需要识别出发送消息的主体，即认证发送消息的主体。
以上三个方面表明：通信时，得建立一些标准的协议来确保传输消息的完整性与时效性，还可以确保消息来源是可靠的且通信实体是真实的，可以避免被骗，伪装等攻击，这些规范的协议就是认证协议。随着认证理论和技术的迅速发展，各种认证协议不断推出，认证协议的种类也越来越多。
5.单密钥加密体制
说起这个，又不得不提单密钥加密的密钥分配，是不是很熟悉，第五章有
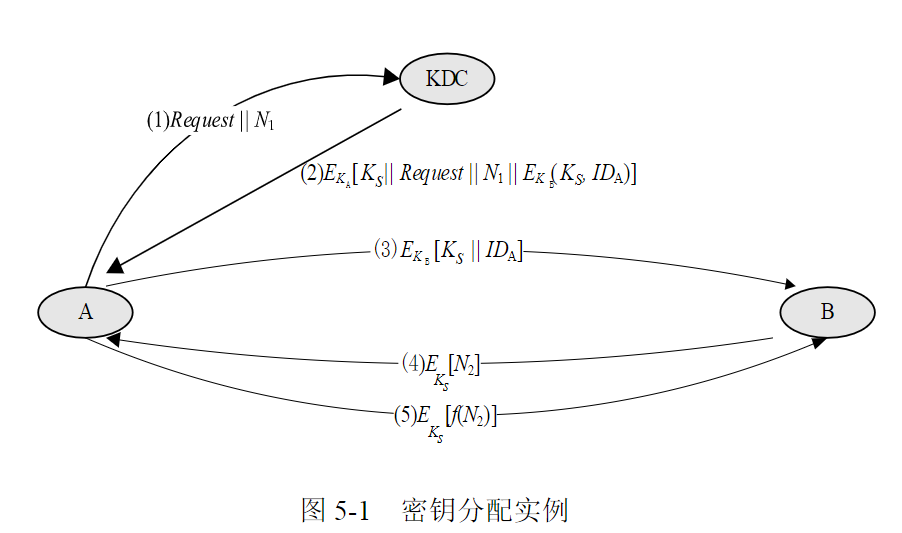
还是拿出这个图，解释一下A告诉中间机构 KDC 我想加密啦（其中包括一个随机数），KDC收到给他回复收到（是由A密钥加密的，所以只有A知道内容是什么，内容包括一个短暂会话密钥Ks，和那个随机数N{说明确实是A联系的}），并且给他一个附件（相同的会话密钥Ks，和A的身份，这俩一块用Kb加密），然后A把刚刚的附件发给B（对吧，这个只有B能打开，而且包含A的身份和会话密钥），B表示我收到啦，用会话密钥加密一个随机数发给A，A说好的好的，用这个数的函数变换加密后回复，后来他俩说什么，就只有他俩知道了，这就是经典的单钥加密的密钥传输，但是有个问题，在A收到KDC附件并进行转发的时候，容易受到重放攻击。
什么是重放攻击？过了过了，这个就先翻篇了，
6.再看公钥加密体制
其实也显而易见，一个道理，把随机数变成时间戳，走到这里，这样的图基本就能读懂了，不再赘述了就
第八章 后记
走到这里，后面基本就不考了，我简单提两嘴后面的
密码协议是指利用密码工具实现与安全相关的协议或函数的计算
可证明安全性是将密码系统的安全性归结为某个经过深入研究的数学难题（如大整数素因子分解、计算离散对数等），数学难题被证明求解困难。这种评估方法存在的问题是8它只说明了这个密码方法的安全性与某个困难问题相关，没有完全证明问题本身的安全性。
还是放心不下重放攻击：又称重播攻击。是指攻击者发送一个目的主机已接收过的包，来达到欺骗系统的目的，主要用于身份认证过程，破坏认证的正确性，是不是和刚刚提到的历程很契合，其实即使做出这方面调整，后续也还是有缺陷，只是不会考的，没有再提了。
这门课走到这里基本就结束了。中间笔记的格式我就不再调了，耽误时间。起初只是想粗略地学一下，一点没听过课是，想争取速通一下网课，但是网上竟然没有一个是契合的，而且中间遇到一点小问题还无法解决，最终我决定，用一整天的时间把我的学习历程总结下来，告诉自己还是有学习能力的，一门课再难，一整天也是可以学完的！（下午就开始疲惫了，第二天继续）截至现在，一共历时15小时，到中后期，我觉得我甚至开始喜欢学习了，过程是非常愉快的，以后有机会再系统学习吧。
总之，我可以，你也可以，道阻且长，虽千万人吾往矣。
