该文献的作者是清华大学的高飞飞老师,于2019年11月发表在IEEE COMMUNICATIONS LETTERS上。
文章给出了当用户位置到信道的映射是双射时上行到下行的确定映射函数;还提出了一个稀疏复值神经网络( sparse complex-valued neural network,SCNet)来逼近映射函数,SCNet直接根据预估的上行链路CSI预测下行链路CSI,不需要下行链路训练,也不需要上行链路反馈。
1 研究背景
在大规模MIMO中,BS使用CSI用于波束形成、用户调度等,UE使用CSI用于信号检测,但由于下行链路训练和上行链路反馈相关的开销过高,因此需要进行优化工作。
由于BS和用户的信道只有很小的角度扩展,并且信道尺寸非常大,所以MIMO信道在角域上表现出稀疏性。因为在大规模MIMO中方便获取上行CSI,所有许多研究从上行CSI反馈中获取下行CSI的信息,从而减少下行训练开销和上行反馈开销,如基于CS的方法和基于DL的方法。
与以上两种方法不同,这篇文献提出了一种稀疏复值神经网络(SCNet)用于FDD大规模MIMO的下行CSI预测,主要的贡献有:
- 得出了当位置到信道映射为双射时,给定通信环境下的确定上行到下行的映射函数,还证明了该映射函数可以用前馈网络以任意小的误差来逼近;
- 提出了预测MIMO下行链路CSI的SCNet,适用于具有复值表示的复值函数逼近。
2 系统模型
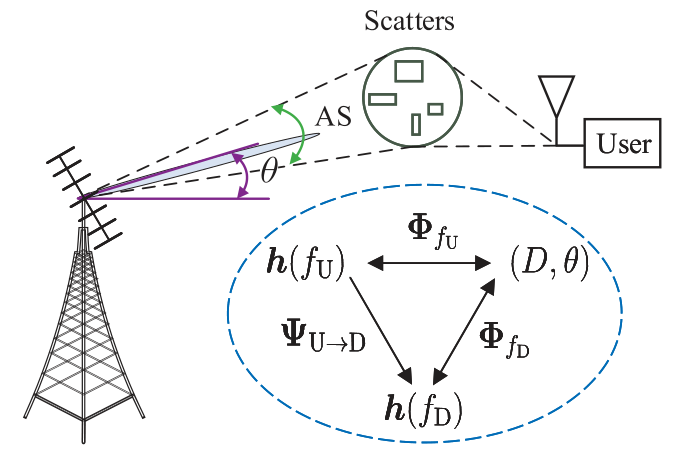
图1 FDD大规模MIMO的下行CSI预测
如图1所示,考虑FDD大规模MIMO系统,BS有M根均匀线性阵列(ULA)天线,UE处为单天线,由于提出的方法可以适用于不同的UE,因此只需要对单个UE进行说明。设UE和BS之间的信道\(h\)由P个射线组成,表示为:
\[\boldsymbol{h}(f)=\sum_{p=1}^{P} \alpha_{p} e^{-j 2 \pi f \tau_{p}+j \phi_{p}} \boldsymbol{a}\left(\theta_{p}\right),\]
其中\(f,\alpha_{p}, \phi_{p}, \tau_{p}\) 和 \(\theta_{p}\)分别为第P条路径的频率、衰减、相移、延迟和到达方向(DOA),\(\boldsymbol{a}\left(\theta_{p}\right)\)为阵列流形向量:
\[\boldsymbol{a}\left(\theta_{p}\right)=\left[1, e^{-j \chi \sin \theta_{p}}, \cdots, e^{-j \chi(M-1) \sin \theta_{p}}\right]^{T}\]
其中\(\chi=2 \pi d f / c\), \(d\)为天线间距,\(c\)为光速,平均DOA \(\theta_{p} \in[\theta-\Delta \theta / 2, \theta+\Delta \theta / 2]\)。
路径衰减\(\alpha_{p}\)取决于:
- UE与BS之间的距离;
- 发射和接收天线的增益;
- 载波频率;
- 散射环境。
相位\(\phi_{p}\)取决于散射体材料和波在散射体处的入射角,延迟 \(\tau_{p}\) 取决于信号沿P路径传播的距离。
3 信道映射函数
用\(\boldsymbol{h}\left(f_{\mathrm{U}}\right)\)和\(\boldsymbol{h}\left(f_{\mathrm{D}}\right)\) 表示上行和下行信道,\(f_{\mathrm{U}}\)和\(f_{\mathrm{D}}\)表示上行和下行频率,由于下行链路和上行链路有相同的传播环境和共同的物理路径,并且无线信道的空间传播特性在一定带宽内几乎不变,因此上行链路和下行链路CSI之间存在着内在的联系。文献首先定义了一个上行到下行的映射函数,并证明了它的存在性,然后利用深度学习来找到这个映射函数。
3.1 上下行信道映射的存在性
如公式(1)所示,信道函数由参数\(\alpha_{p}\), \(\phi_{p}, \tau_{p}, P, \Delta \theta\) 和 \(\theta\)决定。
定义1:位置到信道的映射\(\Phi_{f}\)可以写成:
\[\boldsymbol{\Phi}_{f}:\{(D, \theta)\} \rightarrow\{\boldsymbol{h}(f)\},\]
其中集合\(\{(D, \theta)\}\) 和 \(\{\boldsymbol{h}(f)\}\)分别是映射\(\Phi_{f}\)的域和上域。
假设1:位置到通道的映射函数(3)\(\boldsymbol{\Phi}_{f}:\{(D, \theta)\} \rightarrow\{\boldsymbol{h}(f)\}\)是双射的。
假设1意味着每个用户位置都有一个唯一的通道函数\(\boldsymbol{h}(f)\),每个信道函数也对应唯一的用户位置。在实际无线通信场景中,$$\Phi_{f}$$为双射的概率在实际中是非常高的,并且随着BS处天线数量的增加,该概率趋于1,因此在大规模MIMO系统中采用假设1是合理的。信道到位置的映射,即\(\Phi_{f}\)的逆映射表示为:
\[\boldsymbol{\Phi}_{f}^{-1}:\{\boldsymbol{h}(f)\} \rightarrow\{(D, \theta)\},\]
命题1:根据假设1,对于给定的通信环境,存在上行到下行的映射可以写成:
\[\boldsymbol{\Psi}_{\mathrm{U} \rightarrow \mathrm{D}}=\boldsymbol{\Phi}_{f_{\mathrm{D}}} \circ \boldsymbol{\Phi}_{f_{\mathrm{U}}}^{-1}:\left\{\boldsymbol{h}\left(f_{\mathrm{U}}\right)\right\} \rightarrow\left\{\boldsymbol{h}\left(f_{\mathrm{D}}\right)\right\},\]
其中\(\boldsymbol{\Phi}_{f_{\mathrm{D}}} \circ \boldsymbol{\Phi}_{f_{U}}^{-1}\) 表示\(\boldsymbol{\Phi}_{f_{\mathrm{D}}}\) 和\(\boldsymbol{\Phi}_{f_{\mathrm{U}}}^{-1}\)相关的复合映射。
证明:根据定义1,得到在候选集\(\{(D, \theta)\}\)中存在\(\boldsymbol{\Phi}_{f_{\mathrm{D}}}:\{(D, \theta)\} \rightarrow\left\{\boldsymbol{h}\left(f_{\mathrm{D}}\right)\right\}\)和\(\boldsymbol{\Phi}_{f_{\mathrm{U}}}:\{(D, \theta)\} \rightarrow\left\{\boldsymbol{h}\left(f_{\mathrm{U}}\right)\right\}\)的映射。在假设1下,映射\(\boldsymbol{\Phi}_{f_{U}}^{-1}\)存在,其上域等于\(\boldsymbol{\Phi}_{f_{\mathrm{D}}}\)的域。因此,复合映射 \(\boldsymbol{\Phi}_{f_{\mathrm{D}}} \circ \boldsymbol{\Phi}_{f_{\mathrm{U}}}^{-1}\)存在于\(\{(D, \theta)\}\)。
3.2 用于上下行信道映射的深度学习
命题1证明上下行信道映射的存在性,根据万能近似定理,得到定理1:
定理1:对于给定任意小的误差 \(\varepsilon>0\),总存在一个足够大的正常数\(N\)使:
\[\sup _{\boldsymbol{x} \in \mathbb{H}}\left\|\operatorname{NET}_{N}(\boldsymbol{x}, \boldsymbol{\Omega})-\boldsymbol{\Psi}_{\mathrm{U} \rightarrow \mathrm{D}}(\boldsymbol{x})\right\| \leq \varepsilon, \quad \mathbb{H}=\left\{\boldsymbol{h}\left(f_{\mathrm{U}}\right)\right\}\]
其中\(\operatorname{NET}_{N}(\boldsymbol{x}, \boldsymbol{\Omega})\)是三层前馈网络的输出,\(\boldsymbol{x}, \Omega\) 和 \(N\) 分别表示输入数据、网络参数和隐藏单元数。
根据定理1,具有单个隐藏层的前馈网络可以以任意小的误差逼近上行到下行的映射函数。因此,我们可以训练深度学习网络从上行CSI预测出下行CSI,并且可以使用离线训练,显著降低下行训练和上行反馈所需的开销。
4 基于SCNet的下行CSI预测4.1 SCNet的网络结构
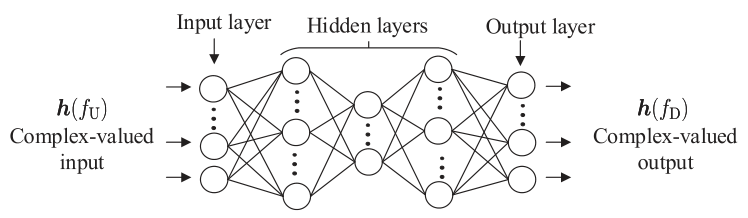
图2 SCNet的网络结构
如图2所示,SCNet的输入为上行CSI矩阵\(\boldsymbol{h}\left(f_{\mathrm{U}}\right)\),输出是\(\boldsymbol{h}\left(f_{\mathrm{U}}\right)\)的非线性变换级联,即:
\[\hat{\boldsymbol{h}}\left(f_{\mathrm{D}}\right)=\operatorname{NET}\left(\boldsymbol{h}\left(f_{\mathrm{U}}\right), \boldsymbol{\Omega}\right)=\boldsymbol{f}^{(L-1)}\left(\cdots \boldsymbol{f}^{(1)}\left(\boldsymbol{h}\left(\left(f_{\mathrm{U}}\right)\right)\right),\right)\]
其中\(L\)为网络层数,\(\boldsymbol{\Omega} \triangleq\left\{\boldsymbol{W}^{(l)}, \boldsymbol{b}^{(l)}\right\}_{l=1}^{L-1}\) 为待训练的网络参数。\(f^{(l)}\)是是第\(l\)层的非线性变换函数,写作:
\[\boldsymbol{f}^{(l)}(\boldsymbol{x})= \begin{cases}\boldsymbol{g}\left(\boldsymbol{W}^{(l)} \boldsymbol{x}+\boldsymbol{b}^{(l)}\right), & 1 \leq l<L-1 ; \\ \boldsymbol{W}^{(l)} \boldsymbol{x}+\boldsymbol{b}^{(l)}, & l=L-1,\end{cases}\]
\(g\)为激活函数:
\[\boldsymbol{g}(\boldsymbol{z})=\max \{\Re[\boldsymbol{z}], \mathbf{0}\}+j \max \{\Im[\boldsymbol{z}], \mathbf{0}\}\]
\(\Re[\cdot]\) 和 \(\Im[\cdot]\)为信道向量的实部与虚部。
在SCNet中,中间隐藏层的神经元数量比输出层中的神经元数量少得多,作为SCNet的压缩输入功能。由于上行信道\(\boldsymbol{h}\left(f_{\mathrm{U}}\right)\)存在稀疏结构,SCNet能够发现大规模MIMO系统中\(\boldsymbol{h}\left(f_{\mathrm{U}}\right)\)的固有稀疏性。因此SCNet不仅可以减少网络参数的冗余,而且性能和鲁棒性更强。
4.2 SCNet的训练和部署
文章提出的下行CSI预测分为离线训练和在线部署两个阶段。
在离线训练阶段,BS同时采集下行和上行CSI作为训练样本,对SCNet进行训练。具体来说,在一个相干时间内,下行CSI首先在UE端通过下行训练进行估计,然后反馈给BS,上行CSI则通过上行训练在BS处估计。对SCNet网络进行训练,使输出\(\hat{\boldsymbol{h}}\left(f_{\mathrm{D}}\right)\)与标签\(\boldsymbol{h}\left(f_{\mathrm{D}}\right)\)之间的差异最小化。损失函数为:
\[\operatorname{Loss}(\boldsymbol{\Omega})=\frac{1}{V N_{h}} \sum_{v=0}^{V-1}\left\|\hat{\boldsymbol{h}}\left(f_{\mathrm{D}}\right)^{(v)}-\boldsymbol{h}\left(f_{\mathrm{D}}\right)^{(v)}\right\|_{2}^{2},\]
其中\(V\)为批大小,上标(\(v\))为第\(v\)个训练样本,\(\|\cdot\|_{2}\)为\(\ell_{2}\)范数,\(N_h\)为向量\(\boldsymbol{h}\left(f_{\mathrm{D}}\right)\)的长度。利用复杂设计自适应矩估计(ADAM)算法最小化损失函数直到SCNet收敛。
在部署阶段,SCNet的参数是固定的,SCNet直接根据上行CSI \(\boldsymbol{h}\left(f_{\mathrm{U}}\right)\) 生成下行链路CSI \(\hat{\boldsymbol{h}}\left(f_{\mathrm{D}}\right)\) 的预测值。
5 实验结果
BS配置由128根天线,上行频率遵循3GPP R15标准\(f_{\mathrm{U}}=2.5 \mathrm{GHz}\)。在5.1中,每条路径的衰减服从瑞利分布,相位和延迟在\([-\pi, \pi)\) 和\(\left[0,10^{-4}\right] s\)内均匀分布,在训练和部署阶段路径的数量都是200条;在5.2中,每条路径的参数是根据射线追踪模拟器生成的,训练阶段路径数为200条,部署阶段路径数不同。
把SCNet与FNN对比,FNN最初是为大规模MIMO系统的上行/下行信道校准而设计的,也可用于FDD大规模MIMO系统的下行信道预测。选择隐藏层的神经元个数为\((128,64,128)\),ADAM算法的初始学习率为0.001,批大小为128,网络分别对每个AS度和每个下行频率进行训练,训练样本数为102400个,epoch数为400个。
5.1 预测精度分析
用归一化均方误差(NMSE)来衡量预测精度:
\[\mathrm{NMSE}=E\left[\left\|\boldsymbol{h}_{\mathrm{D}}-\hat{\boldsymbol{h}}_{\mathrm{D}}\right\|_{2}^{2} /\left\|\boldsymbol{h}_{\mathrm{D}}\right\|_{2}^{2}\right]\]
图3为不同的AS下,上下行频率差分别为120 MHz和480 MHz时SCNet和FNN的性能比较。可以看到随着AS的增加,SCNet和FNN的NMSE性能下降,NMSE曲线的斜率随AS的增加而减小。这是因为随着AS的增加,信道在角域中的稀疏度降低,网络学习信道结构和准确预测信道CSI的难度增大,而且在AS较大情况下,网络对AS的敏感性较低,这是宽AS情况下斜率减小的原因。
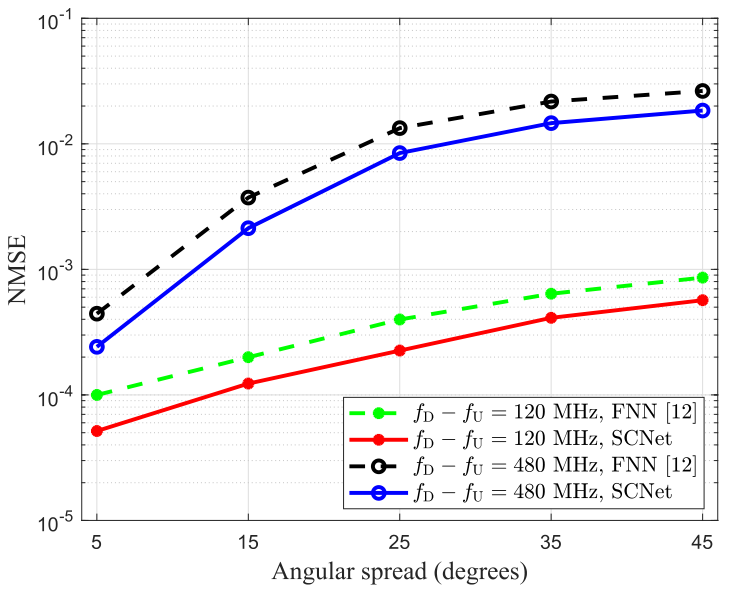
图3 SCNet和FNN的NMSE与不同AS的关系
图4为不同频率差\(f_{\mathrm{D}}-f_{\mathrm{U}}\)下,AS分别为\(5°\)和\(45°\)时SCNet和FNN的性能比较。可以看出,随着频率差的增加SCNet和FNN的性能都有所下降。这是因为上行链路和下行链路之间的CSI相关性随着频率差的增加而趋于消失。
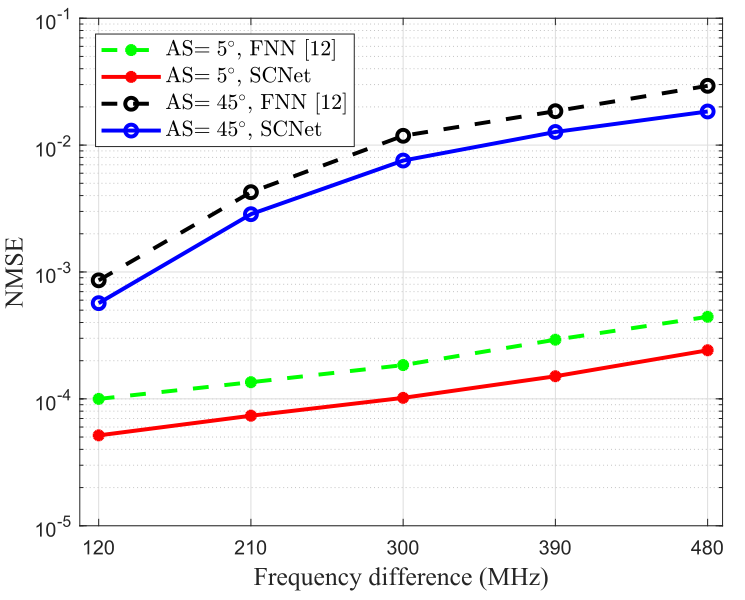
图4 SCNet和FNN的NMSE与不同频率差的关系
由图3、图4可以看出SCNet在所有场景下都优于FNN,验证了SCNet可以从复杂表示提供的丰富表示能力中受益。
5.2 鲁棒性分析
在5.1中,通道是基于公式(1)生成的,具有相同的统计量。然而现实中的信道环境可能更加复杂,训练阶段和部署阶段的统计不匹配也是不可避免的。为了测试SCNet和FNN的鲁棒性,使用不同场景下Wireless InSite[2]生成的数据进行训练和测试。
如图4所示,训练阶段的路径数为200条,部署阶段的路径数有140~260条。结果表明,信道统计量的变化会导致性能下降,但SCNet较FNN仍然具有预测精度的性能优势,验证了深度神经网络良好的泛化能力。
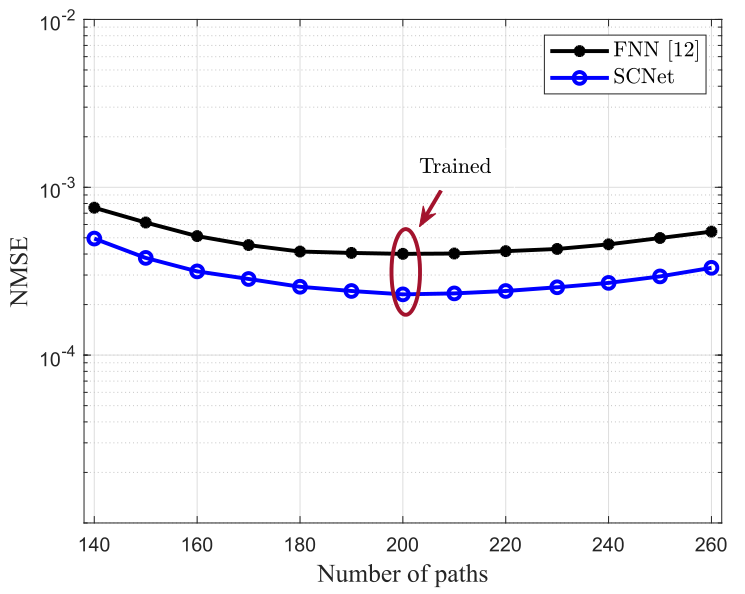
图5 SCNet和FNN的NMSE与不同路径数的关系6 结论
文献得出了在给定的通信环境中存在一个确定的上行到下行链路映射函数;然后提出了用于下行CSI预测的SCNet。
仿真结果表明,SCNet在预测精度方面优于FNN,它对无线信道预测也有较强的鲁棒性。
重要文献
[1] C. Huang, G. C. Alexandropoulos, A. Zappone, C. Yuen, and M. Debbah, “Deep learning for UL/DL channel calibration in generic massive MIMO systems,” in Proc. IEEE Int. Conf. Commun. (ICC),Shanghai, China, Mar. 2019, pp. 1–6.
[2] Remcom Wireless Insite. Accessed: Apr. 2019. [Online]. Available:https://www.remcom.com/wireless-insite-em-propagation-software