一、背景编码是信息处理的基础（重新表示信息）。普通的编码是等长编码，例如7位的ASCIL编码，对出现频率不同的字符都使用相同的编码长度。但其在传输和存储等情况下编码效率不高。可使用不等长编码，来压缩编码：高频字符编码长度更短，低频字符编码长度更长。[例] 将百分制的考试成绩转换成五分制的成绩
按顺序分别编码。
按频率分别编码（高频短编码，类似于香农熵衡量随机变量的编码长度下界）。这种贪心思想，可以找到一种平均最短编码长度-霍夫曼编码。可将构造平均最短编码转化为，构造平均查找长度最小的编码树（构造更有效的搜索树）二、哈夫曼树哈夫曼树的定义
带权路径长度就是所有叶子节点的编码长度乘以权重的和。 希望权重越高的叶子节点，编码长度越小。[例] 有五个叶子结点，它们的权值为{1,2,3,4,5}，用此权值序列可以构造出形状不同的多个二叉树。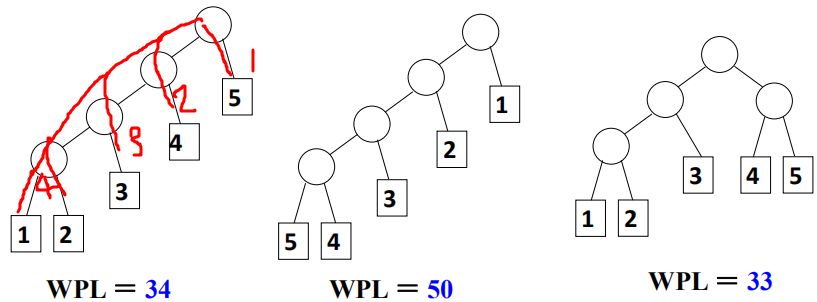
哈夫曼树的构造初始全是只有一个节点的树构成的森林 （优先队列存放树的根节点，每次合并后将新的树插入队列）
每次把权值最小的两棵二叉树合并 （自底向上）使用最小堆，Huffman树为二叉树
typedef struct TreeNode *HuffmanTree;struct TreeNode{ int Weight; HuffmanTree Left, Right;};/* WPL WeightPathLength Cost越小编码越有效， O(NlogN) */ HuffmanTree Huffman( MinHeap H ){ /* 假设H->Size个权值已经存在H->Elements[]->Weight里 */ int i; HuffmanTree T; BuildMinHeap(H); /* 将H->Elements[]按权值调整为最小堆 */ /* 做 H->Size - 1 次合并 */ for (i = 1; i Size; i++) { T = malloc( sizeof( struct TreeNode) ); /* 建立新结点 */ T->Left = DeleteMin(H); /* 从最小堆中删除一个结点，作为新T的左子结点 */ T->Right = DeleteMin(H); /* 从最小堆中删除一个结点，作为新T的右子结点 */ T->Weight = T->Left->Weight + T->Right->Weight; /*计算新权值*/ Insert( H, T ); /*将新T插入最小堆*/ } T = DeleteMin(H); return T;int WPL( HuffmanTree H ){ return H->Weight;}
哈夫曼树的特点
- 没有度为1的结点；
- 哈夫曼树的任意非叶节点的左右子树交换后仍是哈夫曼树；
- n个叶子结点的哈夫曼树共有2n-1个结点；
对同一组权值{w1 ,w2, …… , wn}，是否存在不同构的两棵哈夫曼树呢？存在，当存在相同权值的根节点时。对一组权值{ 1, 2 , 3, 3 }}，不同构的两棵哈夫曼树：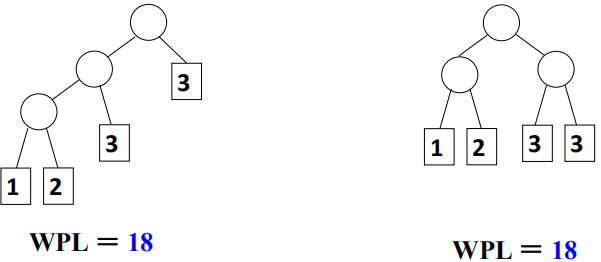
哈夫曼编码给定一段字符串，如何对字符进行编码，使得该字符串的编码存储空间最少？[例] 假设有一段文本，包含58个字符，并由以下7个字符构：a，e，i， s，t，空格（sp），换行（nl）；这7个字符出现的次数不同。如何对这7个字符进行编码，使得总编码空间最少？[分析]（1）用等长ASCII编码：58 ×8 = 464位；（2）用等长3位编码：58 ×3 = 174位；（3）不等长编码：出现频率高的字符用的编码短些，出现频率低的字符则可以编码长些？怎么进行不等长编码？如何避免二义性？
- 前缀码prefix code：任何字符的编码，都不是另一字符编码的前缀
可以无二义地解码（判定字符是否都在叶结点上，没有字符在路径上，不然解码时会有歧义）用二叉树进行编码：1）左右分支：0、1; 2）字符只在叶结点上[例] 四个字符的频率: a:4, u:1, x:2, z:1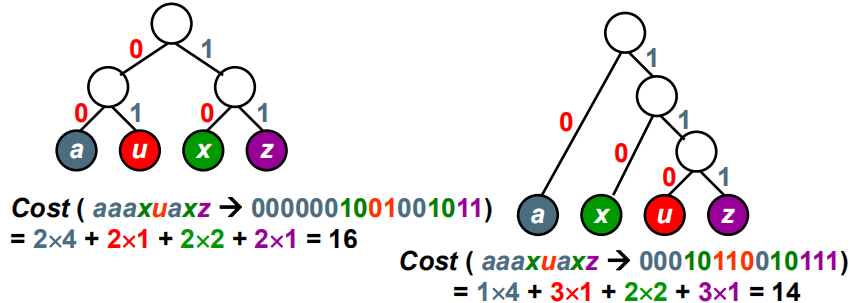
〖例〗哈夫曼编码
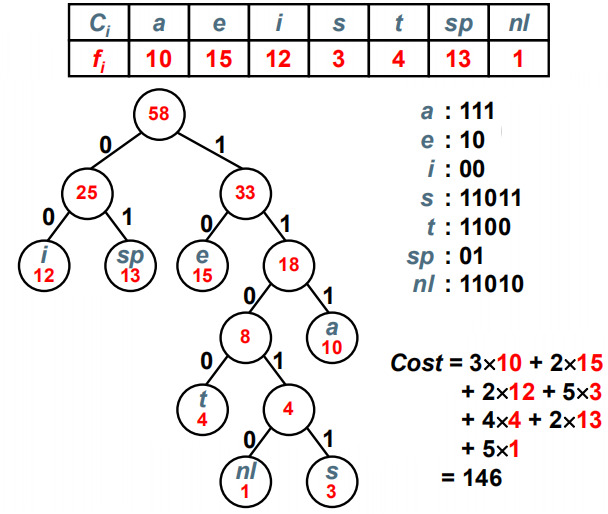题外话，这种使用优先队列的方法，在层次聚类里也有。