Java栈和队列·上
- 1. 栈(Stack)
- 1.1 概念
- 1.2 实现
- 1.3用法
- 1.4栈练习题
大家好,我是晓星航。今天为大家带来的是 Java栈和队列·上 的讲解!
1. 栈(Stack)
1.1 概念
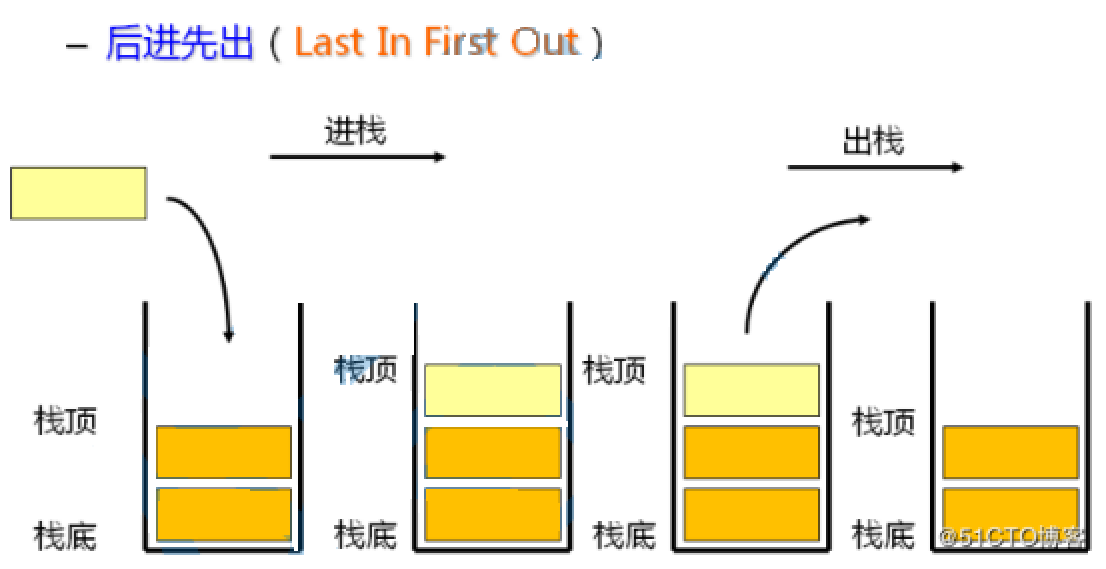
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
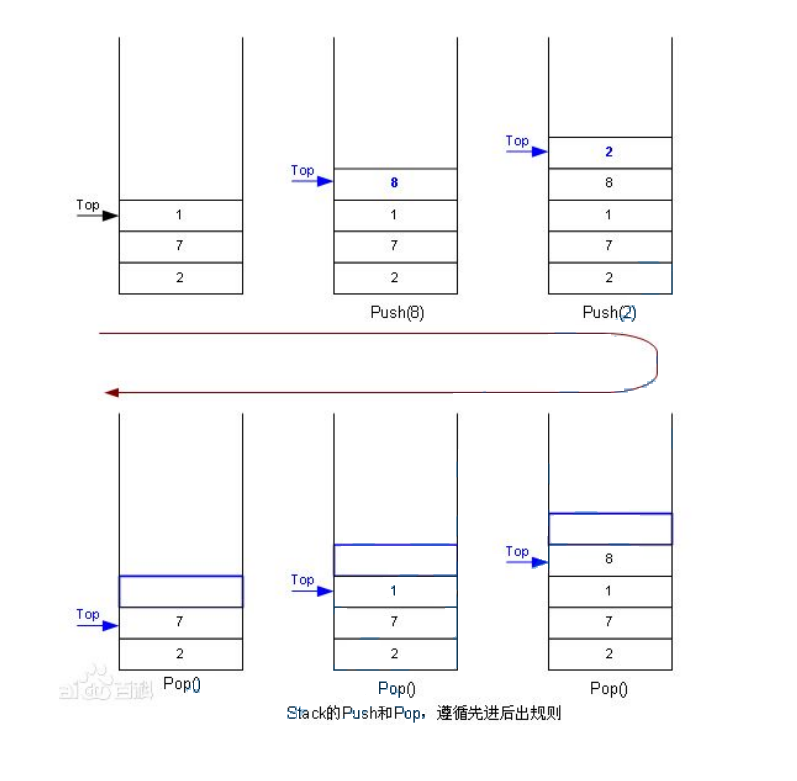
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据在栈顶。(先进去的后出)
那么什么是栈帧呢?
答:我们调用函数时,计算机会为这个函数开辟一块内存,即为栈帧。在JVA stack上开辟。
提问:能不能用单链表实现栈?

1.2 实现
- 利用顺序表实现,即使用尾插 + 尾删的方式实现
- 利用链表实现,则头尾皆可
相对来说,顺序表的实现上要更为简单一些,所以我们优先用顺序表实现栈。
public class TestDemo { // 简单起见,我们就不考虑扩容问题了 private int[] array = new int[100]; private int size = 0; public void push(int v) { array[size++] = v; } public int pop() { return array[--size]; } public int peek() { return array[size - 1]; } public boolean isEmpty() { return size == 0; } public int size() { return size; }}push:增加栈中元素(压栈-在栈顶插入)
pop:弹出栈顶元素,并且删除
peek:获取栈顶元素,但是不删除
empty:判断栈中元素是否为空,为空返回true,不为空返回flase。
size:获取栈中元素个数,并返回数值
isEmpty:判断栈中元素是否为空,为空返回true,不为空返回flase。(继承于Vector父类)
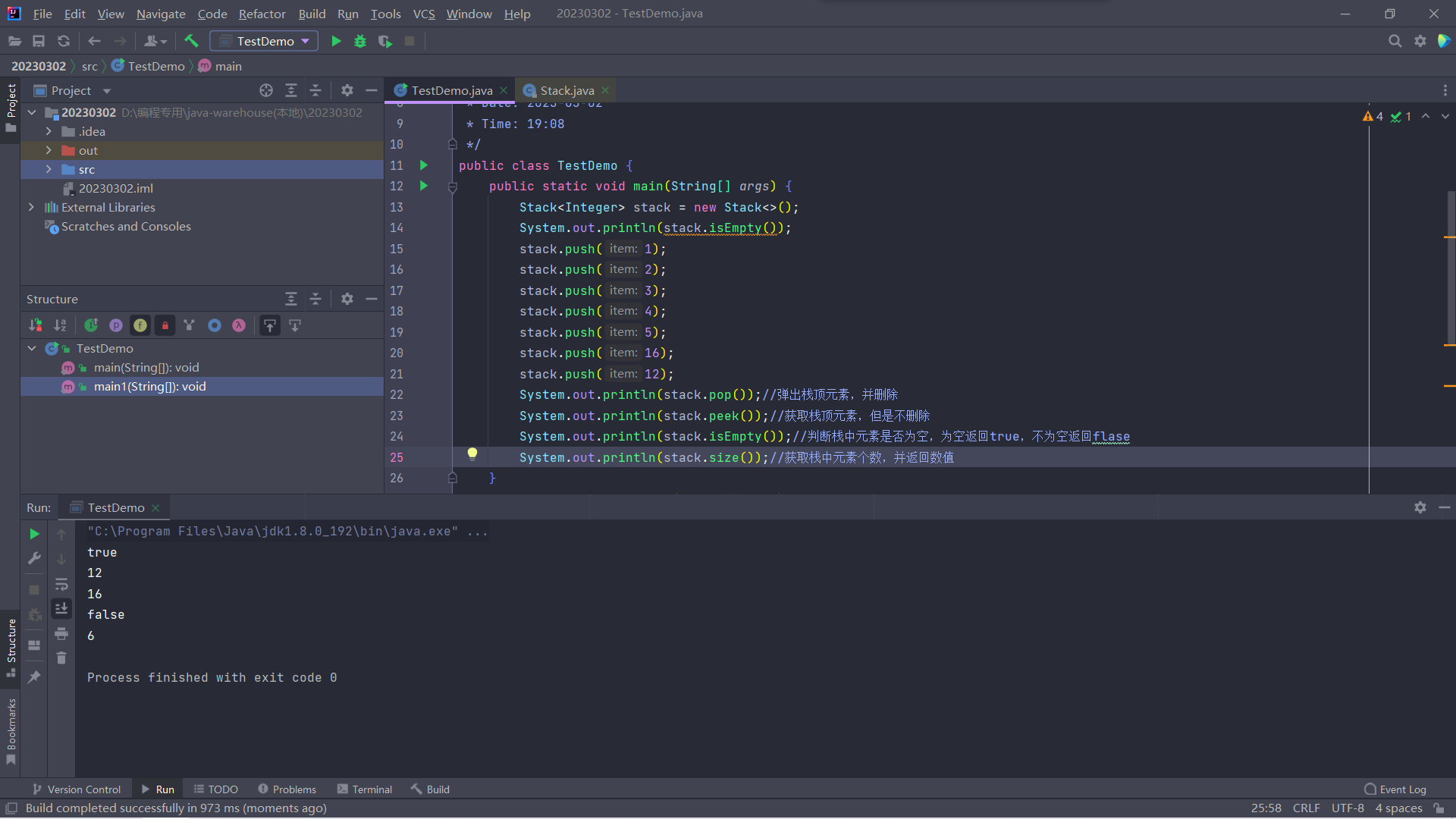
代码示意图如上
自己实现栈:
import java.util.Arrays;public class MyStack { public int[] elem; public int useSize; public MyStack() { this.elem = new int[5]; } public void push(int val) { if(isFull()) { //扩容 this.elem = Arrays.copyOf(this.elem,2*this.elem.length); } this.elem[this.useSize] = val; useSize++; } public boolean isFull() { return this.useSize == this.elem.length; } public int peek() { if (isEmpty()) { throw new RuntimeException("栈为空"); } return this.elem[useSize - 1]; } public int pop() { if (isEmpty()) { throw new RuntimeException("栈为空"); } int oldVal = this.elem[useSize-1]; this.useSize--; return oldVal; } public boolean isEmpty() { return this.useSize == 0; }} 
1.3用法
1、入栈和出栈的顺序?
例如:一个栈的入栈序列是a、b、c、d、e则栈不可能的输出序列是:()
A.edcba B.decba C.dceab D.abcde
答:选C。
解析:这里我们后入的先出,但不一定要全部入进去才能出,所以例如选项D可以入一个出一个。
2、已知一个栈的入栈序列是mnxyz,则不可能出现的出栈顺序是?
A.mnxyz B.xnyzm C.nymxz D.nmyzx
答:选C
解析:这里和上面第一题解法相同也是后入的先出,随进随出,而C不符合这个规律,因此C错误。
3、中缀表达式 转 后缀表达式:
(5+4)*3-2
(((5+4)*3)-2)
(((54)+3)*2)-
54+3*2-
如何通过 这个后缀 表达式 来计算一个值呢?
具体图解过程如下:
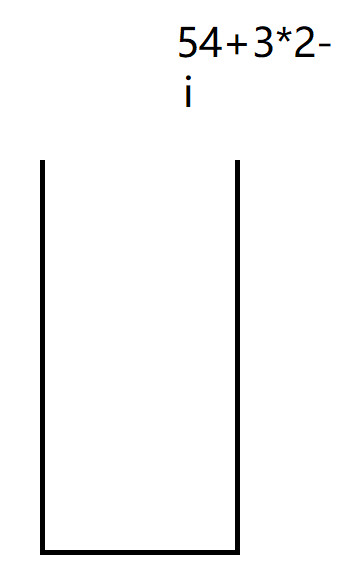
i开始遍历我们的表达式:
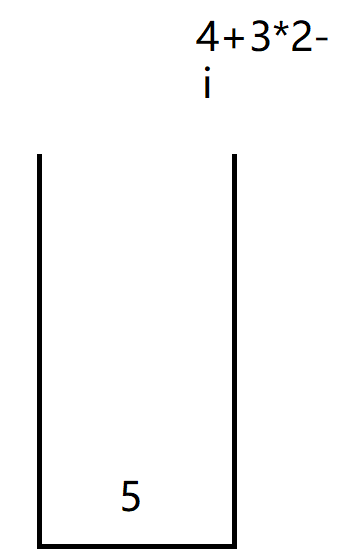
i遍历到4,并将5放入栈中
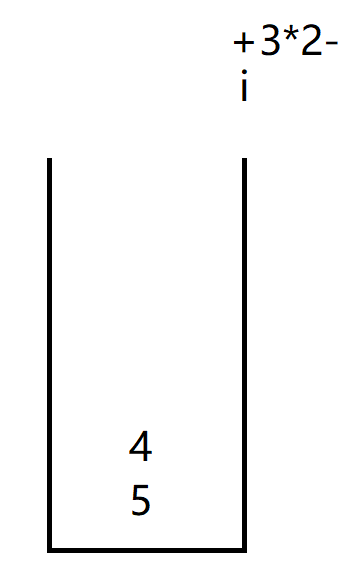
i遍历到+,并将4放入栈中

此时因为i访问到了+号,因此开始计算前面两个元素的值,先入栈的放左边后入栈的放右边。

将计算好的结果9放入栈中,i继续向后走遇到3
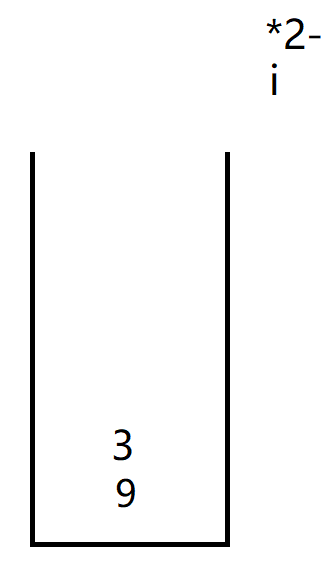
i遍历到*,并将3放入栈中

此时因为i访问到了*号,因此开始计算前面两个元素的值,先入栈的放左边后入栈的放右边。

将计算好的结果27放入栈中,i继续向后走遇到2

i遍历到-,并将2放入栈中
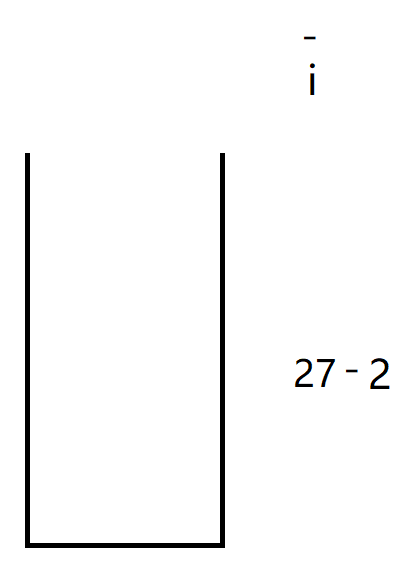
此时因为i访问到了-号,因此开始计算前面两个元素的值,先入栈的放左边后入栈的放右边。
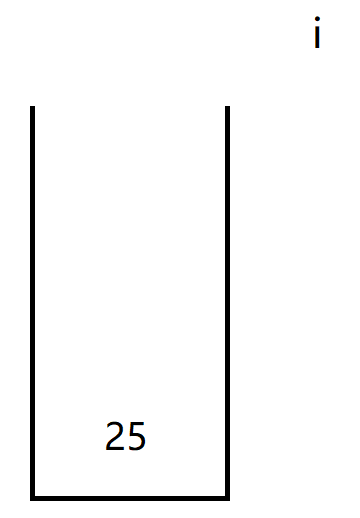
i往后走没有值停下,此时将计算好的结果25放入栈中
上述便是计算机计算后缀表达式的详细图解过程
转化方法为先按照计算顺序分别加上括号,然后再按照符号的顺序将他们分别放在各自的括号后面(后缀表达式)
如果此时是将中缀表达式 转 前缀表达式 则为:-*+54 3 2 (过程如下)
(5+4)*3-2
(((5+4)*3)-2)
-(*(+(54)3)2)
-*+54 3 2
如何用代码来实现中缀表达式转化为后缀表达式呢?
1.定义很多的常量,来标识每个运算符的优先级( ) + – * /
2.借助栈
下面为大家带来一个使用栈来计算后缀表达式的编程题目:
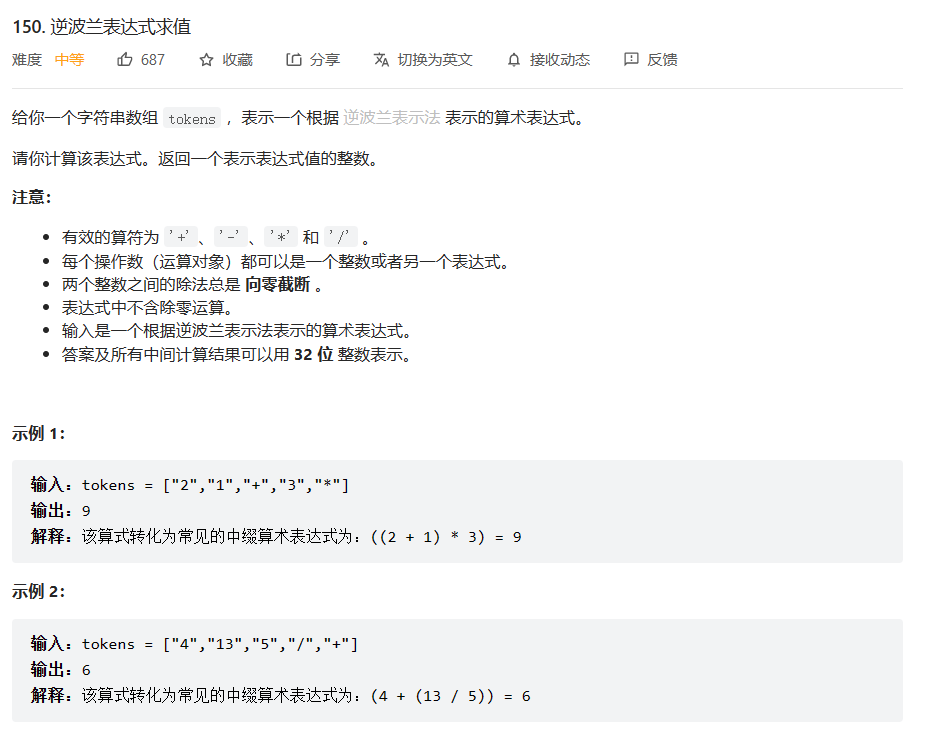
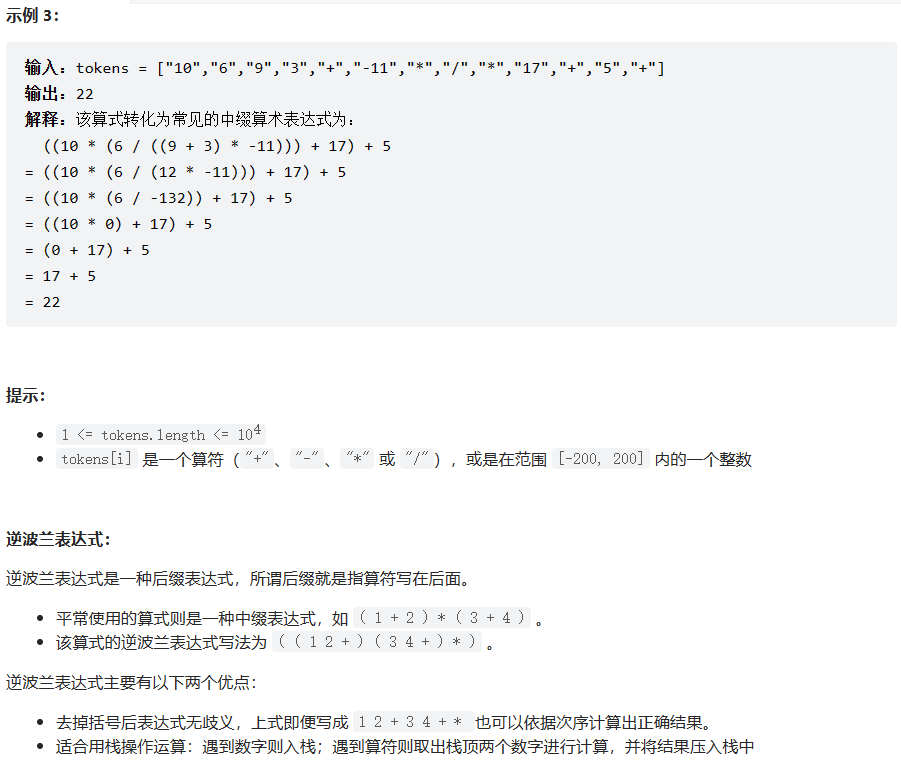
class Solution { public int evalRPN(String[] tokens) { Stack<Integer> stack = new Stack<>(); for (int i = 0; i < tokens.length; i++) { String val = tokens[i]; if (!isOperation(val)) { //如果不是运算符 stack.push(Integer.parseInt(val)); } else { //如果是运算符 int num2 = stack.pop(); int num1 = stack.pop(); switch (val) { case "+": stack.push(num1+num2); break; case "-": stack.push(num1-num2); break; case "*": stack.push(num1*num2); break; case "/": stack.push(num1/num2); break; } } } return stack.pop(); } private boolean isOperation(String x) { if (x.equals("+") || x.equals("-") || x.equals("*") || x.equals("/")) { return true; } return false; }} 
下面题目是通过计算机来计算出栈与入栈的可能性:


1、遍历pushA数组,存放元素到栈中。
2、获取栈顶元素和当前j下标元素是否一样?
3、如果一样哪么就弹出,j++ ……
注意事项:
1、栈是否为空?
import java.util.ArrayList;public class TestDemo { public boolean IsPopOrder (int [] pushA,int [] popA) { Stack<Integer> stack = new Stack<>(); int j = 0; for (int i = 0; i < pushA.length; i++) { stack.push(pushA[i]); while (j < popA.length && stack.empty() && stack.peek() == popA[j]) { stack.pop(); j++; } } return stack.empty(); }} 1.4栈练习题
- 括号匹配问题。OJ链接
import java.util.Stack;class Solution { public boolean isValid(String s) { Stack<Character> stack = new Stack<>(); for (int i = 0; i < s.length(); i++) { char ch = s.charAt(i); if (ch == '(' || ch == '[' || ch == '{' ) { //如果是左括号直接入栈 stack.push(ch); } else { //如果是右括号 if (stack.empty()) { //右括号多 System.out.println("右括号多!"); return false; } char top = stack.peek(); if (top == '(' && ch == ')' || top == '[' && ch == ']' || top == '{' && ch == '}') { //如果左括号和右括号匹配 则弹出这个左括号 stack.pop(); } else { //左右括号不匹配 System.out.println("左右括号不匹配"); return false; } } } if (!stack.empty()) { //左括号多 System.out.println("左括号多!"); return false; } return true; }}题目描述的很清楚,左右括号如果不匹配,无非是以下几种情况:
1、左括号多余右括号
2、右括号多余左括号
3、左右括号顺序不想匹配
在使用代码将这几种情况考虑完全后,便可轻易通过测试。
思路如下:
如果是左括号我们直接使其进栈,如果是右括号我们先判断右括号是否比左括号多,再看其是否相匹配,匹配则弹出相对应的左括号继续下一个括号的判断,如果不匹配则返回不匹配错误,在右括号全部判断完毕后,我们判断一下栈此时是否为空,如果为空则我们所有的括号都匹配成功即正确,如果不为空则是左括号比右括号要多,我们就返回false。
- 实现一个最小栈。OJ链接


class MinStack { private Stack<Integer> stack; private Stack<Integer> minStack; public MinStack() { stack = new Stack<>(); minStack = new Stack<>(); } public void push(int val) { stack.push(val); if (!minStack.empty()) { int top = minStack.peek(); //比较 小于等于的话 也要放进来 if (val <= top) { minStack.push(val); } } else { minStack.push(val); } } public void pop() { int popVal = stack.pop(); if (!minStack.empty()) { int top = minStack.peek(); if (top == popVal) { minStack.pop(); } } } public int top() { return stack.peek(); } public int getMin() { return minStack.peek(); }}思路:这里我们采取了使用两个栈(一个普通栈 一个最小栈)来比较的方法,例如我们在push元素时,普通栈我们是直接放进去的,而最小栈我们则是通过比较,如果要放的元素比我们最小栈栈顶的元素小或等于我们便在最小栈也放入一份。
在pop弹出栈顶元素时我们同样是直接弹出普通栈的栈顶元素,然后比较这个弹出的元素和最小栈栈顶元素的大小是否相等,如果相等我们则还需要再pop一次最小栈的栈顶元素。
top方法和我们stack栈中的peek方法一样,我们直接返回stack的peek方法即可。
getMin方法是返回栈中最小元素,我们这里有两个栈,而最小栈的原理就是将最小的元素通过压栈(头插)的方式进入最小栈,因此我们最小栈的最小值永远是栈顶的元素,我们直接返回最小栈的栈顶元素即可。

感谢各位读者的阅读,本文章有任何错误都可以在评论区发表你们的意见,我会对文章进行改正的。如果本文章对你有帮助请动一动你们敏捷的小手点一点赞,你的每一次鼓励都是作者创作的动力哦!